题目内容
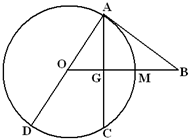 如图,已知AD为圆O的直径,直线BA与圆O相切于点A,直线OB与弦AC垂直并相交于点G,与弧AC相交于M,连接DC,AB=10,AC=12.
如图,已知AD为圆O的直径,直线BA与圆O相切于点A,直线OB与弦AC垂直并相交于点G,与弧AC相交于M,连接DC,AB=10,AC=12.(1)求证:BA•DC=GC•AD;
(2)求OA.
考点:与圆有关的比例线段
专题:立体几何
分析:(1)要证BA•DC=GC•AD,只需证
=
,由OG⊥AC,得GC=AG;即证
=
,由Rt△AGB∽Rt△DCA即可;
(2)由AC得AG,由AB求得BG;由Rt△AGB~Rt△DCA,求得AD,即圆的直径,从而得OA的值.
| BA |
| AD |
| GC |
| DC |
| BA |
| AD |
| AG |
| DC |
(2)由AC得AG,由AB求得BG;由Rt△AGB~Rt△DCA,求得AD,即圆的直径,从而得OA的值.
解答:
解:(1)证明:∵AC⊥OB,∴∠AGB=90°;
又AD是⊙O的直径,∴∠DCA=90°;
又∵∠BAG=∠ADC(弦切角等于同弧所对的圆周角),
∴Rt△AGB∽Rt△DCA;
∴
=
;
又∵OG⊥AC,∴GC=AG;
∴
=
,即BA•DC=GC•AD.
(2)∵AC=12,∴AG=6;
∵AB=10,∴BG=
=8;
由(1)知,Rt△AGB~Rt△DCA,
∴
=
,
∴AD=15,即圆的直径2r=15,
∴OA=7.5.
又AD是⊙O的直径,∴∠DCA=90°;
又∵∠BAG=∠ADC(弦切角等于同弧所对的圆周角),
∴Rt△AGB∽Rt△DCA;
∴
| BA |
| AD |
| AG |
| DC |
又∵OG⊥AC,∴GC=AG;
∴
| BA |
| AD |
| GC |
| DC |
(2)∵AC=12,∴AG=6;
∵AB=10,∴BG=
| AB2-AG2 |
由(1)知,Rt△AGB~Rt△DCA,
∴
| AB |
| AD |
| BG |
| AC |
∴AD=15,即圆的直径2r=15,
∴OA=7.5.
点评:本题考查了与圆有关的几何证明和计算问题,也考查了逻辑推理能力与空间想象能力,是基础题目.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
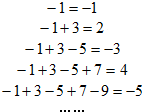 观察如图所示5个等式:照图中式子规律:
观察如图所示5个等式:照图中式子规律: