题目内容
已知点A(3,-4),B(6,3),C(5-m,3+m).
(1)若点A,B,C是一个三角形的三个顶点,求实数m应满足的条件;
(2)若△ABC是以A为直角顶点的直角三角形,求实数m的值.
(1)若点A,B,C是一个三角形的三个顶点,求实数m应满足的条件;
(2)若△ABC是以A为直角顶点的直角三角形,求实数m的值.
考点:数量积判断两个平面向量的垂直关系
专题:平面向量及应用
分析:由已知写出向量
与
,
(1)由向量共线求出m的值,则使A、B、C三点能构成三角形的实数m应满足的条件可求.
(2)利用向量垂直的充要条件列出方程求出m.
| AB |
| AC |
(1)由向量共线求出m的值,则使A、B、C三点能构成三角形的实数m应满足的条件可求.
(2)利用向量垂直的充要条件列出方程求出m.
解答:
解:∵A(3,-4),B(6,3),C(5-m,3+m),
∴
=(3,7),
=(2-m,7+m),
(1)若A、B、C三点能构成三角形,
则向量
与
不共线.由3×(7+m)-7×(2-m)=0得:m=-
.
所以A、B、C三点能构成三角形的实数m应满足m≠-
.
(2)若△ABC是以A为直角顶点的直角三角形,
∴
⊥
,
∴3(2-m)+7(7+m)=0,解得m=-
.
∴
| AB |
| AC |
(1)若A、B、C三点能构成三角形,
则向量
| AB |
| AC |
| 7 |
| 10 |
所以A、B、C三点能构成三角形的实数m应满足m≠-
| 7 |
| 10 |
(2)若△ABC是以A为直角顶点的直角三角形,
∴
| AB |
| AC |
∴3(2-m)+7(7+m)=0,解得m=-
| 55 |
| 4 |
点评:本题考查向量垂直的充要条件、向量共线的充要条件、利用向量共线解决三点共线问题、三点不共线问题.

练习册系列答案
相关题目
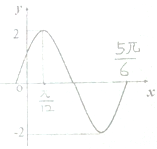 函数f(x)=Asin(ωx+φ)(ω>0,|φ|<
函数f(x)=Asin(ωx+φ)(ω>0,|φ|<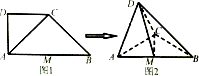 如图1,在四边形ABCD中,AD⊥CD,CD∥AB,AB=2AD=2CD=4,M为线段AB的中点,将△ADC沿AC折起,使平面ADC⊥平面ABC,得到几何体D-ABC,如图2,所示.
如图1,在四边形ABCD中,AD⊥CD,CD∥AB,AB=2AD=2CD=4,M为线段AB的中点,将△ADC沿AC折起,使平面ADC⊥平面ABC,得到几何体D-ABC,如图2,所示.