题目内容
1.已知a∈R,函数f(x)=x|x-a|.(Ⅰ)当a=2时,将函数f(x)写成分段函数的形式,并作出函数的简图,写出函数y=f(x)的单调递增区间;
(Ⅱ)当a>2时,求函数y=f(x)在区间[1,2]上的最小值.
分析 (Ⅰ)化简f(x)=x|x-2|=$\left\{\begin{array}{l}{2x-{x}^{2},x≤2}\\{{x}^{2}-2x,x>2}\end{array}\right.$,从而作其图象,并写出单调增区间;
(Ⅱ)化简f(x)=$\left\{\begin{array}{l}{-{x}^{2}+ax,x≤a}\\{{x}^{2}-ax,x>a}\end{array}\right.$,分类讨论以确定函数的单调性,从而比较以确定函数的最小值.
解答 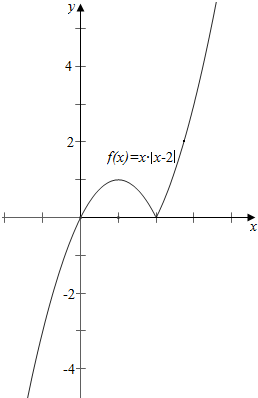 解:(Ⅰ)当a=2时,f(x)=x|x-2|=$\left\{\begin{array}{l}{2x-{x}^{2},x≤2}\\{{x}^{2}-2x,x>2}\end{array}\right.$,
解:(Ⅰ)当a=2时,f(x)=x|x-2|=$\left\{\begin{array}{l}{2x-{x}^{2},x≤2}\\{{x}^{2}-2x,x>2}\end{array}\right.$,
故作其图象如右图,
函数y=f(x)的单调递增区间为(-∞,1],(2,+∞);
(Ⅱ)f(x)=$\left\{\begin{array}{l}{-{x}^{2}+ax,x≤a}\\{{x}^{2}-ax,x>a}\end{array}\right.$,
①当1<$\frac{a}{2}$<2,即2<a<4时,
f(x)在[1,$\frac{a}{2}$]上是增函数,在($\frac{a}{2}$,2]上是减函数;
而f(1)=a-1,f(2)=2a-4,
故f(1)-f(2)=a-1-2a+4=3-a,
故当2<a≤3时,
f(1)≥f(2),
故fmin(x)=f(2)=2a-4;
当3<a<4时,
f(1)<f(2),
故fmin(x)=f(1)=a-1;
②当a≥4时,f(x)在[1,2]上是增函数,
故fmin(x)=f(1)=a-1;
综上所述,fmin(x)=$\left\{\begin{array}{l}{2a-4,2<a≤3}\\{a-1,a>3}\end{array}\right.$.
点评 本题考查了分段函数的应用,同时考查了分类讨论的思想应用及数形结合的思想应用.

 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| 1 | - | ╳ | ╳ | ╳ | ╳ | |||
| 2 | ╳ | - | ╳ | ╳ | ||||
| 3 | ╳ | ╳ | - | ╳ | ╳ | |||
| 4 | ╳ | - | ╳ | |||||
| 5 | ╳ | ╳ | - | ╳ | ||||
| 6 | ╳ | - | ╳ | |||||
| 7 | ╳ | ╳ | ╳ | - | ╳ | |||
| 8 | ╳ | ╳ | - |
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
| A. | 0 | B. | 2 | C. | 3 | D. | 4 |
| A. | y=x2cosx | B. | y=x2sinx | C. | y=2-x | D. | y=|lnx| |
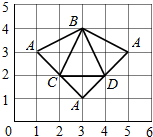
| A. | 2 | B. | $\frac{3}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{2}{3}$ |
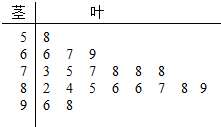 某上市公司为了解A市用户对其产品的满意度,从该市随机调查了20个用户,得到用户对其产品的满意度评分,并用茎叶图记录分数如图所示.
某上市公司为了解A市用户对其产品的满意度,从该市随机调查了20个用户,得到用户对其产品的满意度评分,并用茎叶图记录分数如图所示.