题目内容
6．已知四面体ABCD的侧面展开图如图所示，则其体积为（ ）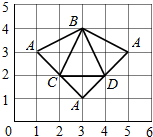
| A． | 2 | B． | $\frac{3}{2}$ | C． | $\frac{3}{4}$ | D． | $\frac{2}{3}$ |
分析 利用展开图判断三棱锥的底面形状，推出棱长，然后求解几何体的体积．
解答 
解：由题意可知三棱锥的底面是等腰直角三角形，腰长为：$\sqrt{2}$，斜边为：2，
3条侧棱相等为：$\sqrt{5}$．
如图：△BOC≌△BOA≌△BOD，
可得BO是三棱锥的高为2．
四面体ABCD的体积为：$\frac{1}{3}×\frac{1}{2}×CD•OA•OB$=$\frac{1}{3}×\frac{1}{2}×2×1×2$=$\frac{2}{3}$．
故选：D．
点评 本题考查几何体的体积的求法，考查计算能力以及空间想象能力．
练习册系列答案
相关题目
16．若双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的一条渐近线平行于直线x+2y+5=0，一个焦点与抛物线y2=-20x的焦点重合，则双曲线的方程为（ ）（ ）
| A． | $\frac{{x}^{2}}{20}$-$\frac{{y}^{2}}{5}$=1 | B． | $\frac{{x}^{2}}{5}$-$\frac{{y}^{2}}{20}$=1 | ||
| C． | $\frac{3{x}^{2}}{25}$-$\frac{3{y}^{2}}{100}$=1 | D． | $\frac{3{x}^{2}}{100}$-$\frac{3{y}^{2}}{25}$=1 |
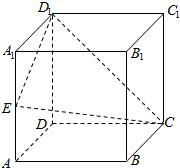如图，有一个正方体的木块，E为棱AA1的中点．现因实际需要，需要将其沿平面D1EC将木块锯开．请你画出前面ABB1A1与截面D1EC的交线，并说明理由．
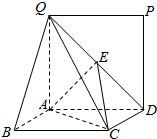如图，矩形ABCD所在的平面与正方形ADPQ所在的平面相互垂直，E是QD的中点．
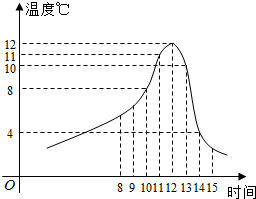某食品的保鲜时间t（单位：小时）与储藏温度x（恒温，单位：℃）满足函数关系$t=\left\{\begin{array}{l}64，x≤0\\{2^{kx+6}}，x＞0.\end{array}\right.$且该食品在4℃的保鲜时间是16小时．