Question

已知二次函数f（x）=x²+mx+n（m、n∈R）的两个零点分别在（0，1）与（1，2）内，则（m+1）²+（n-2）²的取值范围是（　　）

• A、[2，

  5

  ]
• B、(

  2

  ，

  5

  )
• C、[2，5]
• D、（2，5）

Answer 1

考点：简单线性规划,二次函数的性质

专题：计算题,直线与圆

分析：由条件可得，

f(0)＞0 f(1)＜0 f(2)＞0

，化简得到关于m，n的不等式组，在平面直角坐标系中，作出不等式组表示的区域，
再由（m+1）²+（n-2）²表示的几何意义是点（-1，2）到区域内的点的距离的平方，由图象观察，即可得到取值范围．

解答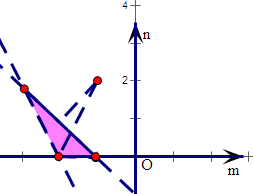： 解：由于二次函数f（x）=x²+mx+n（m、n∈R）的两个零点
分别在（0，1）与（1，2）内，
则

f(0)＞0 f(1)＜0 f(2)＞0

即有

n＞0 1+m+n＜0 4+2m+n＞0

，
在平面直角坐标系中，作出不等式组表示的区域，
而（m+1）²+（n-2）²表示的几何意义是点（-1，2）
到区域内的点的距离的平方，
求得点（-1，2）到直线m+n+1=0的距离为

|-1+2+1|

2

=

2

，
点（-1，2）到点（-2，0）的距离为

5

，
故（m+1）²+（n-2）²的取值范围是（2，5）．
故选D．

点评：本题考查二次函数与二次方程的关系，考查二元不等式表示的平面区域，考查两点的距离和点到直线的距离公式的运用，考查数形结合的思想方法，属于中档题．