题目内容
若函数f(x)=
在区间[a,b](a,b为整数)上的值域是[0,1],则满足条件的数对(a,b)共有 对.
| 2012-|x| |
| |x|+2012 |
考点:函数与方程的综合运用
专题:计算题,函数的性质及应用
分析:讨论x大于等于0时,化简f(x),然后分别令f(x)等于0和1求出对应的x的值,得到f(x)为减函数,根据反比例平移的方法画出f(x)在x大于等于0时的图象,根据f(x)为偶函数即可得到x小于0时的图象与x大于0时的图象关于y轴对称,可画出函数的图象,从函数的图象看出满足条件的整数对有4025个.
解答:
 解:当x≥0时,函数f(x)=
解:当x≥0时,函数f(x)=
,
令f(x)=0,解得x=2012,
令f(x)=1,解得x=0,
易知函数在x>0时为减函数,
利用y=
平移的方法可画出x>0时f(x)的图象,又由此函数为偶函数,
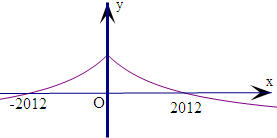
得到x<0时的图象是由x>0时的图象关于y轴对称得来的,所以函数的图象可画为:
根据图象可知满足整数数对的有(-2012,0),(-2012,1),…,(-2012,2012),(-2011,2012),(-2010,2012),(-2009,2012),…,(0,2012)共4025个.
故答案为:4025.
 解:当x≥0时,函数f(x)=
解:当x≥0时,函数f(x)=| 2012-x |
| x+2012 |
令f(x)=0,解得x=2012,
令f(x)=1,解得x=0,
易知函数在x>0时为减函数,
利用y=
| 4024 |
| x |
得到x<0时的图象是由x>0时的图象关于y轴对称得来的,所以函数的图象可画为:
根据图象可知满足整数数对的有(-2012,0),(-2012,1),…,(-2012,2012),(-2011,2012),(-2010,2012),(-2009,2012),…,(0,2012)共4025个.
故答案为:4025.
点评:此题考查学生会利用分类讨论及数形结合的数学思想解决实际问题,掌握函数定义域的求法,是一道中档题.

练习册系列答案
相关题目
已知f(x)=
,则f{f(-2)}的值为( )
|
| A、8 | B、9 | C、2 | D、3 |
已知集合A={1,2,3}.则满足A∪B=A的非空集合B的个数是( )
| A、1 | B、2 | C、7 | D、8 |
设双曲线
-
=1(a>0,b>0)的左、右焦点分别为F1,F2,离心率为e,过F2的直线与双曲线的右支交于A,B两点,若△F1AB是以A为直角顶点的等腰直角三角形,则e2=( )
| x2 |
| a2 |
| y2 |
| b2 |
A、1+2
| ||
B、4-2
| ||
C、5-2
| ||
D、3+2
|
已知二次函数f(x)=x2+mx+n(m、n∈R)的两个零点分别在(0,1)与(1,2)内,则(m+1)2+(n-2)2的取值范围是( )
A、[2,
| ||||
B、(
| ||||
| C、[2,5] | ||||
| D、(2,5) |
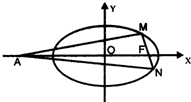 椭圆C:
椭圆C: