题目内容
已知函数f(x)满足f(x+1)=
,且当x∈(0,1]时,f(x)=x,g(x)=m(x+3),若方程f(x)=g(x)在区间(-1,1]上有两个不同的实根,则实数m的取值范围是( )
| 1 |
| f(x)+1 |
A、(0,
| ||
B、(0,
| ||
C、(
| ||
D、(
|
考点:根的存在性及根的个数判断
专题:计算题,作图题,函数的性质及应用
分析:化简当-1<x<0时,f(x)=
-1,从而作出f(x)与g(x)的图象,从而解得.
| 1 |
| x+1 |
解答:
 解:∵f(x+1)=
解:∵f(x+1)=
,且当x∈(0,1]时,f(x)=x,
∴当-1<x<0时,
f(x)=
-1,
故f(x)的图象如实曲线,g(x)的图象过(-3,0),斜率为m,如虚线.
依题意,可知m∈(0,
].
故选A.
 解:∵f(x+1)=
解:∵f(x+1)=| 1 |
| f(x)+1 |
∴当-1<x<0时,
f(x)=
| 1 |
| x+1 |
故f(x)的图象如实曲线,g(x)的图象过(-3,0),斜率为m,如虚线.
依题意,可知m∈(0,
| 1 |
| 4 |
故选A.
点评:本题考查函数解析式的求法及数形结合的思想,属于难题.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
函数f(x)=ax2+2(a-3)x+1在区间[-3,+∞)上递减,则实数a的取值范围是( )
| A、(-∞,0) | ||
B、[-
| ||
C、[-
| ||
| D、(0,+∞) |
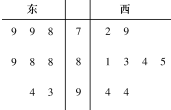 某城市要建成宜商、宜居的国际化新城,该城市的东城区、西城区分别引进8个厂家,现对两个区域的16个厂家进行评估,综合得分情况如茎叶图所示.
某城市要建成宜商、宜居的国际化新城,该城市的东城区、西城区分别引进8个厂家,现对两个区域的16个厂家进行评估,综合得分情况如茎叶图所示.