题目内容
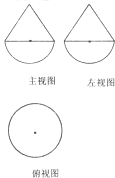已知一个几何体是由上、下两部分构成的组合体，其三视图如图，若图中圆的半径为l，等腰三角形的腰长为| 5 |
考点：由三视图求面积、体积
专题：空间位置关系与距离
分析：根据几何体的三视图知该几何体是上部为圆锥，底面为半球的组合体，求出它的表面积即可．
解答：
解：根据几何体的三视图得，
该几何体是上部为圆锥，底面为半球的组合体，
∴该几何体的表面积是
S=πrl+2πr2=π×1×
+2π×12=2π+
π．
故答案为：2π+
π．
该几何体是上部为圆锥，底面为半球的组合体，
∴该几何体的表面积是
S=πrl+2πr2=π×1×
| 5 |
| 5 |
故答案为：2π+
| 5 |
点评：本题考查了空间几何体的三视图的应用问题，解题时应根据三视图得出该几何体是什么图形，从而解答问题．
练习册系列答案
点睛新教材全能解读系列答案
小学教材完全解读系列答案
相关题目
函数f（x）=ax2+2（a-3）x+1在区间[-3，+∞）上递减，则实数a的取值范围是（ ）
| A、（-∞，0） | ||
B、[-
| ||
C、[-
| ||
| D、（0，+∞） |
平面向量
=（-1，1），
=(1，2)，且
•
=3，则
•
=（ ）
| AB |
| n |
| n |
| AC |
| n |
| BC |
| A、-2 | B、2 | C、3 | D、4 |
如图，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的体积为（ ）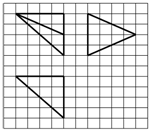
A、
| ||
B、
| ||
C、
| ||
D、
|