题目内容
已知
=9，则tana等于（ ）
| 2sina+cosa |
| sina-3cosa |
| A、-4 | ||
B、-
| ||
C、
| ||
| D、4 |
考点：同角三角函数基本关系的运用
专题：三角函数的求值
分析：已知等式左边分子分母除以cosα，利用同角三角函数间的基本关系化简，整理即可求出tanα的值．
解答：
解：∵
=
=9，
∴tanα=4，
故选：D．
| 2sinα+cosα |
| sinα-3cosα |
| 2tanα+1 |
| tanα-3 |
∴tanα=4，
故选：D．
点评：此题考查了同角三角函数基本关系的运用，熟练掌握基本关系是解本题的关键．
练习册系列答案
相关题目
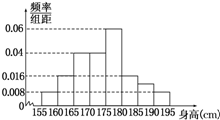从某学校高三年级800名学生中随机抽取50名测量身高，被抽取的学生的身高全部介于155cm和195cm之间，将测量结果按如下方式分成八组：第一组[155，160）；第二组[160，165）；…第八组[190，195]，如图是按上述分组方法得到的频率分布直方图．下列函数中，在定义域内既是奇函数，又是增函数是（ ）
| A、y=sinx |
| B、y=x3-x |
| C、y=2x |
| D、y=x3 |
若g（x）=1-2x，f[g（x）]=(
)x，则f（4）=（ ）
| 1 |
| 3 |
A、
| ||
| B、-27 | ||
| C、9 | ||
D、3
|