题目内容
设a=
(3x2-2x)dx,则(ax2-
)6的展开式中的第4项为( )
| ∫ | 2 1 |
| 1 |
| x |
| A、-1280x3 |
| B、-1280 |
| C、240 |
| D、-240 |
考点:定积分
专题:导数的综合应用,二项式定理
分析:先计算定积分,再写出二项式的通项,即可求得展开式中的第4项.
解答:
解:由于a=
(3x2-2x)dx=(x3-x2)
=4,
则(ax2-
)6的通项为Tr+1=
×(4x2)6-r×(-
)r=(-1)r•
×46-r×x6-3r,
故(ax2-
)6的展开式中的第4项为T3+1=(-1)3•
•46-3•x6-3×3=-1280x3,
故选:A.
| ∫ | 2 1 |
| | | 2 1 |
则(ax2-
| 1 |
| x |
| C | r 6 |
| 1 |
| x |
| C | r 6 |
故(ax2-
| 1 |
| x |
| C | 3 6 |
故选:A.
点评:本题考查定积分知识,考查二项展开式,考查展开式中的特殊项,属于基础题.

练习册系列答案
相关题目
设f(x)=
,则
f(x)dx等于( )
|
| ∫ | 2 0 |
A、
| ||
B、
| ||
C、
| ||
D、
|
“a>1”是“函数y=x2-2ax+a有两个零点”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
已知数列{an}为等差数列,且a4+a5+a6+a7=1,则4a1•4a2…4a10=( )
| A、64 | B、32 | C、16 | D、4 |
已知a∈R,若函数f(x)=x2-|2x-a|有四个零点,则关于x的方程ax2+2x+1=0的实数根的个数为( )
| A、2个 | B、1个 |
| C、0个 | D、与a的取值有关 |
 抛物线y=2x2(-
抛物线y=2x2(-| 6 |
| 6 |
| A、1 | B、2 |
| C、3 | D、AC1 |
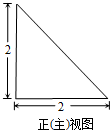 某三棱锥的三视图是三个全等的等腰直角三角形,且正(主)视图如图所示,则此三棱锥的表面积为( )
某三棱锥的三视图是三个全等的等腰直角三角形,且正(主)视图如图所示,则此三棱锥的表面积为( )A、6+2
| ||||
B、4+4
| ||||
C、6+4
| ||||
D、4+4
|