Question

抛物线y=2x²（-

6

≤x≤

6

）绕y轴旋转一周形成一个如图所示的旋转体，在此旋转体内水平放入一个正方体，使正方体的一个面恰好与旋转体的开口面平齐，则此正方体的棱长是（　　）

• A、1
• B、2
• C、3
• D、AC₁

Answer 1

考点：旋转体（圆柱、圆锥、圆台）

专题：空间位置关系与距离

分析：由题意画出过正方体的两条相对侧棱的截面图，设出正方体的棱长，然后利用A点的纵坐标相等列式求解a的值．

解答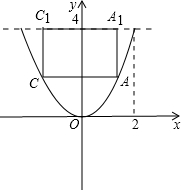： 解：作过正方体的两条相对侧棱的截面图如图，
设正方体AC₁的棱长AA₁=a，则底面对角线AC=

2

a，
∴A点的横坐标等于

2 a

2

，代入抛物线y=2x²得：y=2(

2 a

2

)2=a²，
即A点纵坐标为a²．
抛物线y=2x²（-

6

≤x≤

6

），A₁的纵坐标为：2×(

6

)2=12．
又由题意可知A点纵坐标等于12-a．
∴a²=12-a，解得：a=3．
∴正方体的棱长是3．
故选：C．

点评：本题考查了抛物线的应用，考查了数形结合的解题思想和数学转化思想，能够正确作出该题的截面图是解答该题的关键，属中档题．