题目内容
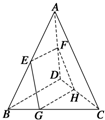 如图,空间四边形ABCD中,E,F分别为AB,AD的中点,G,H分别在BC,CD上,且BG:GC=DH:HC=1:2.下列说法不正确的是( )
如图,空间四边形ABCD中,E,F分别为AB,AD的中点,G,H分别在BC,CD上,且BG:GC=DH:HC=1:2.下列说法不正确的是( )| A、E、F、G、H四点共面 |
| B、GE与HF的交点在直线AC上 |
| C、EF∥面DBC |
| D、GE∥面ADC |
考点:命题的真假判断与应用,直线与平面平行的判定
专题:空间位置关系与距离
分析:由已知条件,结合三角形中位线知识和平行线截线段成比例得到EF∥GH,从而得到E、F、G、H四点共面,结合公理1和公理3得到选项B正确,再由线面平行的判定得到选项C正确,最后反证说明D错误.
解答:
解:如图,
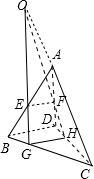
∵E,F分别为AB,AD的中点,
∴EF∥BD,EF=
BD,
∵G,H分别在BC,CD上,且BG:GC=DH:HC,
∴GH∥BD,GH=
BD,
∴EF∥GH,
则E、F、G、H四点共面,选项A正确;
在平面四边形EFHG中,
∵GH>EF,
∴GE交HF于一点,设为O,
则由O∈EG,EG?面ABC,得O∈面ABC,
同理O∈面ACD,
又面ABC∩面ADC=AC,
∴GE与HF的交点在直线AC上,选项B正确;
又EF?面BCD,GH?面BCD,
∴EF∥面BCD,选项C正确;
若GE∥面ADC,则GE∥HF,
∴四边形EFHG为平行四边形,
∴EF=GH,与GH>EF矛盾,
故选:D.

∵E,F分别为AB,AD的中点,
∴EF∥BD,EF=
| 1 |
| 2 |
∵G,H分别在BC,CD上,且BG:GC=DH:HC,
∴GH∥BD,GH=
| 2 |
| 3 |
∴EF∥GH,
则E、F、G、H四点共面,选项A正确;
在平面四边形EFHG中,
∵GH>EF,
∴GE交HF于一点,设为O,
则由O∈EG,EG?面ABC,得O∈面ABC,
同理O∈面ACD,
又面ABC∩面ADC=AC,
∴GE与HF的交点在直线AC上,选项B正确;
又EF?面BCD,GH?面BCD,
∴EF∥面BCD,选项C正确;
若GE∥面ADC,则GE∥HF,
∴四边形EFHG为平行四边形,
∴EF=GH,与GH>EF矛盾,
故选:D.
点评:本题考查命题的真假判断与应用,考查了空间中的线面关系,考查了学生的空间想象能力和思维能力,是中档题.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
已知双曲线
-
=1(a>0,b>0)的焦点为F1、F2,渐近线为l1,l2,过点F2且与l1平行的直线交l2于M,若M在以线段F1 F2为直径的圆上,则双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
| A、2 | ||
B、
| ||
C、
| ||
D、
|
已知函数f(x)=
下列是关于函数y=f[f(x)]+1的零点个数的4个判断:
①当k>0时,有3个零点;
②当k<0时,有2个零点;
③当k>0时,有4个零点;
④当k<0时,有1个零点.
则正确的判断是( )
|
①当k>0时,有3个零点;
②当k<0时,有2个零点;
③当k>0时,有4个零点;
④当k<0时,有1个零点.
则正确的判断是( )
| A、①④ | B、②③ | C、①② | D、③④ |
下列说法正确的是( )
| A、直角坐标系中横、纵坐标相等的点能够组成一个集合 |
| B、π∈{x|x<3,x∈R} |
| C、∅={0} |
| D、{(1,2)}⊆{1,2,3} |
已知O是△ABC所在平面内一点,且2
+
+
=0,则△ABO与△ABC的面积之比为( )
| OA |
| OB |
| OC |
A、
| ||
B、
| ||
C、
| ||
D、
|
给出下列命题:
(1)实数的共轭复数一定是实数;
(2)满足|z-i|+|z+i|=2的复数z在复平面上对应的点的轨迹是椭圆;
(3)若m∈Z,i2=-1,则im+im+1+im+2+im+3=0;
(4)0>-i.
其中正确命题的序号是( )
(1)实数的共轭复数一定是实数;
(2)满足|z-i|+|z+i|=2的复数z在复平面上对应的点的轨迹是椭圆;
(3)若m∈Z,i2=-1,则im+im+1+im+2+im+3=0;
(4)0>-i.
其中正确命题的序号是( )
| A、(1) |
| B、(1)(3) |
| C、(2)(3) |
| D、(1)(4) |
在复平面内,复数z=
(i为虚数单位)的共轭复数等于( )
| 3-i |
| 1+i |
| A、1+2i | B、1-2i |
| C、1+3i | D、-1-3i |