题目内容
下列说法正确的是( )
| A、直角坐标系中横、纵坐标相等的点能够组成一个集合 |
| B、π∈{x|x<3,x∈R} |
| C、∅={0} |
| D、{(1,2)}⊆{1,2,3} |
考点:四种命题,命题的真假判断与应用
专题:计算题,集合
分析:因为直角坐标系中横、纵坐标相等的点是确定的,所以能构成集合;对于B,π=3.14>3;对于C,空集是不含有任何元素的集合;对于D,{(1,2)}表示点集.
解答:
解:对于A,因为直角坐标系中横、纵坐标相等的点是确定的,所以能构成集合;
对于B,π=3.14>3,故不正确;
对于C,空集是不含有任何元素的集合,故C不正确;
对于D,{(1,2)}表示点集,故D不正确.
故选:A.
对于B,π=3.14>3,故不正确;
对于C,空集是不含有任何元素的集合,故C不正确;
对于D,{(1,2)}表示点集,故D不正确.
故选:A.
点评:本题考查了集合中元素的特性,考查集合的概念,考查了确定性,是基础的概念题.

练习册系列答案
相关题目
命题p:x∈R且满足sin2x=1.命题q:x∈R且满足tanx=1.则p是q的( )
| A、充分非必要条件 |
| B、必要非充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
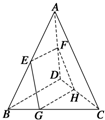 如图,空间四边形ABCD中,E,F分别为AB,AD的中点,G,H分别在BC,CD上,且BG:GC=DH:HC=1:2.下列说法不正确的是( )
如图,空间四边形ABCD中,E,F分别为AB,AD的中点,G,H分别在BC,CD上,且BG:GC=DH:HC=1:2.下列说法不正确的是( )| A、E、F、G、H四点共面 |
| B、GE与HF的交点在直线AC上 |
| C、EF∥面DBC |
| D、GE∥面ADC |
 如图所示,一游泳者自游泳池边AB上的D点,沿DC方向游了10米,∠CDB=60°,然后任意选择一个方向并沿此方向继续游,则他再游不超过10米就能够回到游泳池AB边的概率是( )
如图所示,一游泳者自游泳池边AB上的D点,沿DC方向游了10米,∠CDB=60°,然后任意选择一个方向并沿此方向继续游,则他再游不超过10米就能够回到游泳池AB边的概率是( )A、
| ||
B、
| ||
C、
| ||
D、
|
已知平面向量
,
满足|
|=|
|=2,(
+2
)•(
-
)=-2,则
与
的夹角为( )
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|
 给定两个平面向量
给定两个平面向量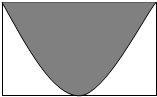 如图,长方形的面积为2,将100颗豆子随机地撒在长方形内,其中恰好有60颗豆子落在阴影部分内,则用随机摸拟的方法可以估计图中阴影部分的面积为( )
如图,长方形的面积为2,将100颗豆子随机地撒在长方形内,其中恰好有60颗豆子落在阴影部分内,则用随机摸拟的方法可以估计图中阴影部分的面积为( )