题目内容
已知O是△ABC所在平面内一点，且2
+
+
=0，则△ABO与△ABC的面积之比为（ ）
| OA |
| OB |
| OC |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点：向量加减混合运算及其几何意义
专题：平面向量及应用
分析：由2
+
+
=0，可得2
+
=-
．如图所示，以
、2
所在的线段OB、OE为邻边作平行四边形OBFE，对角线OF交AB与点D．利用向量的平行四边形法则和平行四边形的性质可得
=
，进而得到
=
，即可得出答案．
| OA |
| OB |
| OC |
| OA |
| OB |
| OC |
| OB |
| OA |
| OD |
| DF |
| 1 |
| 2 |
| OD |
| CD |
| 1 |
| 4 |
解答：
解：由2
+
+
=0，可得2
+
=-
．
如图所示，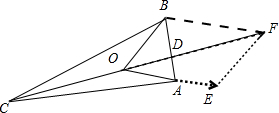
以
、2
所在的线段OB、OE为邻边作平行四边形OBFE，对角线OF交AB与点D．
则
=
=
，
∴
=
，∴
=
．
∴△ABO与△ABC的面积之比=
．
故选：C．
| OA |
| OB |
| OC |
| OA |
| OB |
| OC |
如图所示，
以| OB |
| OA |
则
| OD |
| DF |
| OA |
| BF |
| 1 |
| 2 |
∴
| OD |
| CO |
| 1 |
| 3 |
| OD |
| CD |
| 1 |
| 4 |
∴△ABO与△ABC的面积之比=
| 1 |
| 4 |
故选：C．
点评：本题考查了向量的平行四边形法则和平行四边形的性质、平行线分线段成比例定理、三角形的面积计算公式等基础知识与基本技能方法，属于难题．
练习册系列答案
相关题目
已知变量x，y满足约束条件
，若目标函数z=y+ax仅在点（5，3）处取得最小值，则实数a的取值范围为（ ）
|
| A、（-∞，-1） | ||
| B、（0，+∞） | ||
C、（
| ||
| D、（1，+∞） |
任取实数a、b∈[-1，1]，则a、b满足|a-2b|≤2的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
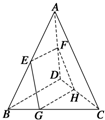如图，空间四边形ABCD中，E，F分别为AB，AD的中点，G，H分别在BC，CD上，且BG：GC=DH：HC=1：2．下列说法不正确的是（ ）| A、E、F、G、H四点共面 |
| B、GE与HF的交点在直线AC上 |
| C、EF∥面DBC |
| D、GE∥面ADC |
设p：“a＞3”q：“f（x）=x3-ax2+1在（0，2）上有唯一零点”，则p是q的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |