题目内容
已知向量
、
满足|
|=1,|
|=
,且(3
-2
)⊥
,则
与
的夹角为 .
| a |
| b |
| a |
| b |
| 3 |
| a |
| b |
| a |
| a |
| b |
考点:数量积表示两个向量的夹角
专题:平面向量及应用
分析:设
与
的夹角为θ,则由题意可得(3
-2
)•
=3-2×1×
cosθ=0,求得cosθ 的值,可得θ 的值.
| a |
| b |
| a |
| b |
| a |
| 3 |
解答:
解:∵向量
、
满足|
|=1,|
|=
,且(3
-2
)⊥
,设
与
的夹角为θ,
∴(3
-2
)•
=3
2-2
•
=3-2×1×
cosθ=0,
求得cosθ=
,∴θ=
,
故答案为:
.
| a |
| b |
| a |
| b |
| 3 |
| a |
| b |
| a |
| a |
| b |
∴(3
| a |
| b |
| a |
| a |
| a |
| b |
| 3 |
求得cosθ=
| ||
| 2 |
| π |
| 6 |
故答案为:
| π |
| 6 |
点评:本题主要考查用两个向量的数量积表示两个向量的夹角,两个向量垂直的性质,属于中档题.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
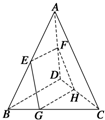 如图,空间四边形ABCD中,E,F分别为AB,AD的中点,G,H分别在BC,CD上,且BG:GC=DH:HC=1:2.下列说法不正确的是( )
如图,空间四边形ABCD中,E,F分别为AB,AD的中点,G,H分别在BC,CD上,且BG:GC=DH:HC=1:2.下列说法不正确的是( )| A、E、F、G、H四点共面 |
| B、GE与HF的交点在直线AC上 |
| C、EF∥面DBC |
| D、GE∥面ADC |
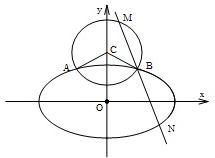 已知离心率为
已知离心率为 给定两个平面向量
给定两个平面向量