题目内容
给出下列命题:
(1)实数的共轭复数一定是实数;
(2)满足|z-i|+|z+i|=2的复数z在复平面上对应的点的轨迹是椭圆;
(3)若m∈Z,i2=-1,则im+im+1+im+2+im+3=0;
(4)0>-i.
其中正确命题的序号是( )
(1)实数的共轭复数一定是实数;
(2)满足|z-i|+|z+i|=2的复数z在复平面上对应的点的轨迹是椭圆;
(3)若m∈Z,i2=-1,则im+im+1+im+2+im+3=0;
(4)0>-i.
其中正确命题的序号是( )
| A、(1) |
| B、(1)(3) |
| C、(2)(3) |
| D、(1)(4) |
考点:复数的基本概念,命题的真假判断与应用
专题:综合题,数系的扩充和复数
分析:(1)实数的虚部为0,所以共轭复数一定是实数;
(2)满足|z-i|+|z+i|=2的复数z在复平面上对应的点的轨迹是线段;
(3)若m∈Z,i2=-1,则im+im+1+im+2+im+3=im(1+i+i2+i3)=0;
(4)0与-i不能比较大小.
(2)满足|z-i|+|z+i|=2的复数z在复平面上对应的点的轨迹是线段;
(3)若m∈Z,i2=-1,则im+im+1+im+2+im+3=im(1+i+i2+i3)=0;
(4)0与-i不能比较大小.
解答:
解:(1)实数的虚部为0,所以共轭复数一定是实数,故(1)正确;
(2)满足|z-i|+|z+i|=2的复数z在复平面上对应的点的轨迹是线段,故(2)不正确;
(3)若m∈Z,i2=-1,则im+im+1+im+2+im+3=im(1+i+i2+i3)=0,故(3)正确;
(4)0与-i不能比较大小,故(4)不正确.
故选:B.
(2)满足|z-i|+|z+i|=2的复数z在复平面上对应的点的轨迹是线段,故(2)不正确;
(3)若m∈Z,i2=-1,则im+im+1+im+2+im+3=im(1+i+i2+i3)=0,故(3)正确;
(4)0与-i不能比较大小,故(4)不正确.
故选:B.
点评:本题考查命题真假判断,考查复数知识,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
命题p:x∈R且满足sin2x=1.命题q:x∈R且满足tanx=1.则p是q的( )
| A、充分非必要条件 |
| B、必要非充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
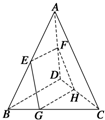 如图,空间四边形ABCD中,E,F分别为AB,AD的中点,G,H分别在BC,CD上,且BG:GC=DH:HC=1:2.下列说法不正确的是( )
如图,空间四边形ABCD中,E,F分别为AB,AD的中点,G,H分别在BC,CD上,且BG:GC=DH:HC=1:2.下列说法不正确的是( )| A、E、F、G、H四点共面 |
| B、GE与HF的交点在直线AC上 |
| C、EF∥面DBC |
| D、GE∥面ADC |
 如图所示,一游泳者自游泳池边AB上的D点,沿DC方向游了10米,∠CDB=60°,然后任意选择一个方向并沿此方向继续游,则他再游不超过10米就能够回到游泳池AB边的概率是( )
如图所示,一游泳者自游泳池边AB上的D点,沿DC方向游了10米,∠CDB=60°,然后任意选择一个方向并沿此方向继续游,则他再游不超过10米就能够回到游泳池AB边的概率是( )A、
| ||
B、
| ||
C、
| ||
D、
|
设函数f(x)=
的定义域为M,函数g(x)=lg(1+x)的定义域为N,则( )
| 1 | ||
|
| A、M∩N=(-1,1] |
| B、M∩N=R |
| C、∁RM=[1,+∞) |
| D、∁RN=(-∞,-1) |