题目内容
已知双曲线
-
=1(a>0,b>0)的焦点为F1、F2,渐近线为l1,l2,过点F2且与l1平行的直线交l2于M,若M在以线段F1 F2为直径的圆上,则双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
| A、2 | ||
B、
| ||
C、
| ||
D、
|
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:已知得出过F且与双曲线C的一条渐近线平行的直线方程,与另一条渐近线方程联立即可解得交点M的坐标,代入以线段F1F2为直径的圆的方程,即可得出离心率e.
解答:
解:不妨设过点F2与双曲线的一条渐过线平行的直线方程为y=
(x-c),
与y=-
x联立,可得交点M(
,-
),
∵点M在以线段F1F2为直径的圆上,
∴
+
=c2,
∴b=
a,
∴c=
=2a,
∴e=
=2.
故选:A.
| b |
| a |
与y=-
| b |
| a |
| c |
| 2 |
| bc |
| 2a |
∵点M在以线段F1F2为直径的圆上,
∴
| c2 |
| 4 |
| b2c2 |
| 4a2 |
∴b=
| 3 |
∴c=
| a2+b2 |
∴e=
| c |
| a |
故选:A.
点评:本题考查双曲线的几何性质,考查学生的计算能力,熟练掌握双曲线的渐近线及离心率、直线的点斜式、圆的方程是解题的关键.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
已知变量x,y满足约束条件
,若目标函数z=y+ax仅在点(5,3)处取得最小值,则实数a的取值范围为( )
|
| A、(-∞,-1) | ||
| B、(0,+∞) | ||
C、(
| ||
| D、(1,+∞) |
命题p:x∈R且满足sin2x=1.命题q:x∈R且满足tanx=1.则p是q的( )
| A、充分非必要条件 |
| B、必要非充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
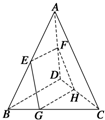 如图,空间四边形ABCD中,E,F分别为AB,AD的中点,G,H分别在BC,CD上,且BG:GC=DH:HC=1:2.下列说法不正确的是( )
如图,空间四边形ABCD中,E,F分别为AB,AD的中点,G,H分别在BC,CD上,且BG:GC=DH:HC=1:2.下列说法不正确的是( )| A、E、F、G、H四点共面 |
| B、GE与HF的交点在直线AC上 |
| C、EF∥面DBC |
| D、GE∥面ADC |