题目内容
在数列{an}中,a1=2,an+1=an+ln(1+
),则a5= .
| 1 |
| n |
考点:数列递推式
专题:等差数列与等比数列
分析:利用累加求和公式an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1及其对数的运算性质即可得出.
解答:
解:∵数列{an}中,a1=1,an+1-an=ln(1+
),
∴an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1
=ln
+ln
+…+ln
+1=ln(
•
•…•
)+2
=lnn+2.
∴a5=ln5+2.
故答案为:ln5+2.
| 1 |
| n |
∴an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1
=ln
| n |
| n-1 |
| n-1 |
| n-2 |
| 2 |
| 1 |
| n |
| n-1 |
| n-1 |
| n-2 |
| 2 |
| 1 |
=lnn+2.
∴a5=ln5+2.
故答案为:ln5+2.
点评:熟练掌握累加求和公式an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1及其对数的运算性质是解题的关键.

练习册系列答案
相关题目
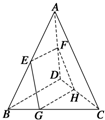 如图,空间四边形ABCD中,E,F分别为AB,AD的中点,G,H分别在BC,CD上,且BG:GC=DH:HC=1:2.下列说法不正确的是( )
如图,空间四边形ABCD中,E,F分别为AB,AD的中点,G,H分别在BC,CD上,且BG:GC=DH:HC=1:2.下列说法不正确的是( )| A、E、F、G、H四点共面 |
| B、GE与HF的交点在直线AC上 |
| C、EF∥面DBC |
| D、GE∥面ADC |
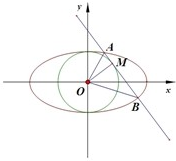 如图,已知椭圆C的方程为
如图,已知椭圆C的方程为