题目内容
已知圆C:x2+y2-4x-2y-15=0上有四个不同的点到直线L:y=k(x-7)+6的距离等于
,则k的取值范围是 .
| 5 |
考点:圆的一般方程
专题:计算题,直线与圆
分析:求出圆心,求出半径,圆心到直线的距离小于半径和
的差即可.
| 5 |
解答:
解:圆x2+y2-4x-2y-15=0的圆心为(2,1),半径为2
,
圆心(2,1)到直线L:y=k(x-7)+6的距离小于
,
∴
<
,∴k的取值范围是(
,2).
故答案为:(
,2).
| 5 |
圆心(2,1)到直线L:y=k(x-7)+6的距离小于
| 5 |
∴
| |-5k+5| | ||
|
| 5 |
| 1 |
| 2 |
故答案为:(
| 1 |
| 2 |
点评:考查圆与直线的位置关系(圆心到直线的距离小于半径和
的差,此时4个,等于3个,大于这个差小于半径和
的和是2个),是基础题.
| 5 |
| 5 |

练习册系列答案
相关题目
双曲线x2-y2=3的渐近线方程为( )
| A、y=±x | ||||
| B、y=±3x | ||||
C、y=±
| ||||
D、y=±
|
设数列{an}的前n项和为Sn,且满足an+Sn=1,则Sn的取值范围是( )
| A、(0,1) | ||
| B、(0,+∞) | ||
C、[
| ||
D、[
|
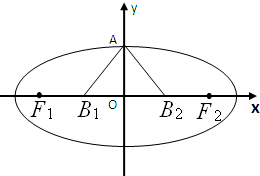 如图,设椭圆C:
如图,设椭圆C: