题目内容
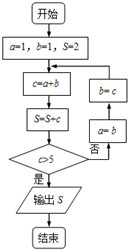
设数列{an}的前n项和为Sn,且满足an+Sn=1,则Sn的取值范围是( )
| A、(0,1) | ||
| B、(0,+∞) | ||
C、[
| ||
D、[
|
考点:数列递推式
专题:等差数列与等比数列
分析:根据条件进行化简,得到{an}是以
为首项,
为公比的等比数列,求出Sn的表达式,即可得到结论.
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:n=1时,a1+S1=2a1=1,
解得a1=
,
n≥2时,
Sn=1-an,Sn-1=1-an-1,
两式相减的
Sn-Sn-1=1-an-1+an-1,
即an=an-1-an,
则2an=an-1,
即
=
,为定值.
数列{an}是以
为首项,
为公比的等比数列.
则Sn=
=1-(
)n,
则1-
≤Sn<1,
即
≤Sn<1,
故选:C
解得a1=
| 1 |
| 2 |
n≥2时,
Sn=1-an,Sn-1=1-an-1,
两式相减的
Sn-Sn-1=1-an-1+an-1,
即an=an-1-an,
则2an=an-1,
即
| an |
| an-1 |
| 1 |
| 2 |
数列{an}是以
| 1 |
| 2 |
| 1 |
| 2 |
则Sn=
| ||||
1-
|
| 1 |
| 2 |
则1-
| 1 |
| 2 |
即
| 1 |
| 2 |
故选:C
点评:本题主要考查递推数列的应用,利用条件判断数列{an}是等比数列是解决本题的关键.

练习册系列答案
相关题目
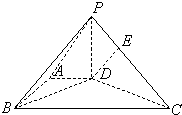 如图,在底面为直角梯形的四棱锥P-ABCD中,AD∥BC,PD⊥平面ABCD,AD=1,AB=
如图,在底面为直角梯形的四棱锥P-ABCD中,AD∥BC,PD⊥平面ABCD,AD=1,AB=| 3 |
(1)求证:BD⊥PC;
(2)设点E在棱PC上,
| FE |
| FC |
若直线x=a是函数f(x)=sinx的一条对称轴,则f(a)=( )
| A、0 | B、1 | C、-1 | D、1或-1 |