题目内容

设集合A={x|0≤x＜1}，B={x|1≤x≤3}，函数f（x）=
3x，x∈A
6-2x，x∈B
，当x0∈A且f[f（x0）]∈A时，x0的取值范围是
 
．
考点：函数的值,分段函数的应用
专题：函数的性质及应用
分析：由已知条件得f[f（x0）]=6-2•3x0，且0≤6-2•3x0＜1，由此能求出x0的取值范围．
解答： 解：∵x0∈A，∴f（x0）=3x0∈[1，3），
∴f[f（x0）]=6-2•3x0，
∵f[f（x0）]∈A，
∴0≤6-2•3x0＜1，
∴
5
2
＜3x0≤3，
∴x0的取值范围是（log3
5
2
，1]．
故答案为：（log3
5
2
，1]．
点评：本题考查实数的取值范围的求法，是基础题，解题时要注意对数性质的合理运用．
练习册系列答案
相关题目
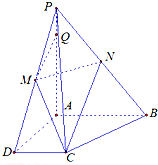已知四棱锥P-ABCD中，PA⊥平面ABCD，且PA=4，底面为直角梯形，∠CDA=∠BAD=90°，AB=2，CD=1，AD=
2
，M，N分别是PD，PB的中点．
（1）设Q为线段AP上一点，若MQ∥平面PCB，求CQ的长； 
（2）求平面MCN与底面ABCD所成锐二面角的大小．
已知0＜x＜1，则x2（1-x）的最大值是
 
．
已知正三棱锥的侧面均为等腰直角三角形，侧面的面积为
1
2
，则它的外接球体积为
 
．
已知函数y=
π
2
-
1
2
arccosx，它的值域是
 
．
双曲线C：
x2
3
-y2=1的左、右焦点分别为F1，F2，直线l过F2，且交双曲线C的右支于A，B（A点在B点上方）两点，若
OA
+2
OB
+3
OF1
=0，则直线的斜率k=
 
．
已知
a
=（2，-1，3），
b
=（-1，4，-2），
c
=（7，5，λ），若
a
，
b
，
c
三向量共面，则λ=
 
．
用1，2，3，4，5，6组成没有重复数字的六位数，要求1与2相邻，3与4相邻，5与6不相邻，这样的六位数共有
 
个．
己知双曲线
x2
a2
-
y2
b2
=1（a＞0，b＞0）离心率为2，有一个焦点与抛物线y2=4x的焦点重合，则ab的值为（　　）
A、
16
3
B、
4
3
3
C、
3
16
D、
3
4

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网