题目内容
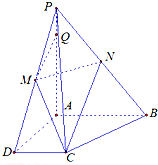 已知四棱锥P-ABCD中,PA⊥平面ABCD,且PA=4,底面为直角梯形,∠CDA=∠BAD=90°,AB=2,CD=1,AD=
已知四棱锥P-ABCD中,PA⊥平面ABCD,且PA=4,底面为直角梯形,∠CDA=∠BAD=90°,AB=2,CD=1,AD=| 2 |
(1)设Q为线段AP上一点,若MQ∥平面PCB,求CQ的长;
(2)求平面MCN与底面ABCD所成锐二面角的大小.
考点:用空间向量求平面间的夹角,直线与平面平行的判定
专题:综合题,空间位置关系与距离,空间角
分析:(1)以A为原点,以AD,AB,AP分别为x,y,z轴建立空间直角坐标系O-xyz,求出Q的坐标,即可求CQ的长;
(2)求出面ABCD的法向量、面MCN的法向量,利用向量的有关运算求出向量的夹角,进而转化为二面角的平面角.
(2)求出面ABCD的法向量、面MCN的法向量,利用向量的有关运算求出向量的夹角,进而转化为二面角的平面角.
解答:
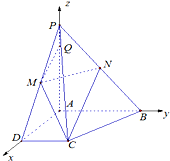 解:(1)因为PA⊥平面ABCD,∠BAD=90°,所以以A为原点,以AD,AB,AP分别为x,y,z轴建立空间直角坐标系O-xyz,
解:(1)因为PA⊥平面ABCD,∠BAD=90°,所以以A为原点,以AD,AB,AP分别为x,y,z轴建立空间直角坐标系O-xyz,
又因为∠ADC=90°,PA=4,AB=2,CD=1,AD=
,M,N分别是PD,PB的中点,所以有A(0,0,0),B(0,2,0),C(
,1,0),D(
,0,0),P(0,0,4),M(
,0,2),N(0,1,2),
因为Q为线段AP上一点,所以可设Q(0,0,t),
则
=(
,-1,0),
=(0,2,-4),
=(-
,0,t-2),
设平面PBC的法向量为
=(x,y,z),
则有:
令z=1,则x=
,y=2⇒
=(
,2,1),
又因为MQ∥平面PCB,所以
•
=(-
,0,t-2)•(
,2,1)=0,得t=3,
从而得Q(0,0,3),故CQ=2
.
(2)设平面MCN的一个法向量为
=(x,y,z),
又
=(-
,-1,2),
=(-
,0,2),
则有:
令z=1,则x=
,y=1⇒
=(
,1,1),又
=(0,0,4)为平面ABCD的一个法向量,
所以cos<
,
>=
=
=
,故平面MCN与底面ABCD所成锐二面角的大小为
.
 解:(1)因为PA⊥平面ABCD,∠BAD=90°,所以以A为原点,以AD,AB,AP分别为x,y,z轴建立空间直角坐标系O-xyz,
解:(1)因为PA⊥平面ABCD,∠BAD=90°,所以以A为原点,以AD,AB,AP分别为x,y,z轴建立空间直角坐标系O-xyz,又因为∠ADC=90°,PA=4,AB=2,CD=1,AD=
| 2 |
| 2 |
| 2 |
| ||
| 2 |
因为Q为线段AP上一点,所以可设Q(0,0,t),
则
| BC |
| 2 |
| PB |
| MQ |
| ||
| 2 |
设平面PBC的法向量为
| n0 |
则有:
|
令z=1,则x=
| 2 |
| n0 |
| 2 |
又因为MQ∥平面PCB,所以
| MQ |
| n0 |
| ||
| 2 |
| 2 |
从而得Q(0,0,3),故CQ=2
| 3 |
(2)设平面MCN的一个法向量为
| n |
又
| CM |
| ||
| 2 |
| CN |
| 2 |
则有:
|
令z=1,则x=
| 2 |
| n |
| 2 |
| AP |
所以cos<
| n |
| AP |
| ||||
|
|
| 4 |
| 2×4 |
| 1 |
| 2 |
| π |
| 3 |
点评:解决此类问题的关键是熟悉几何体的结构特征建立空间直角坐标系,进而利用空间向量的有关运算解决长度、体积、空间角等问题.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
 如图:已知四面体A-BCD的外接球的球心O在线段BD上,且AO⊥平面BCD,BC=
如图:已知四面体A-BCD的外接球的球心O在线段BD上,且AO⊥平面BCD,BC=