题目内容
已知⊙O：x2+y2=1，⊙M：x2+y2+4x-4y+4=0的位置关系是（ ）
| A、外离 | B、外切 | C、内含 | D、相交 |
考点：圆与圆的位置关系及其判定
专题：直线与圆
分析：求出两圆的圆心，根据圆与圆的位置关系的判断即可得到结论．
解答：
解：，⊙M：x2+y2+4x-4y+4=0的标准方程为（x+2）2+（y-2）2=4，圆心M（-2，2），半径R=2，
x2+y2=1的圆心O（0，0），半径r=1，
则|OM|=
=
=2
，
∵2-1＜|OM|＜2+1，
∴⊙O：x2+y2=1，⊙M：x2+y2+4x-4y+4=0位置关系是相交，
故选：D．
x2+y2=1的圆心O（0，0），半径r=1，
则|OM|=
| (-2)2+22 |
| 8 |
| 2 |
∵2-1＜|OM|＜2+1，
∴⊙O：x2+y2=1，⊙M：x2+y2+4x-4y+4=0位置关系是相交，
故选：D．
点评：本题主要考查圆与圆的位置关系的判断，求出两圆的圆心和半径是解决本题的关键．
练习册系列答案
一线名师权威作业本系列答案
相关题目
已知a=20.6，b=0.60，c=log21，则实数a，b，c的大小关系是（ ）
| A、b＞a＞c |
| B、a＞c＞b |
| C、a＞b＞c |
| D、c＞a＞b |
下列命题为真命题的是（ ）
| A、若ac＞bc，则a＞b | ||||
| B、若a2＞b2，则a＞b | ||||
C、若
| ||||
D、若
|
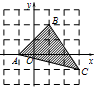已知点A（-1，0），B（1，2），C（3，-1），点P（x，y）为△ABC边界及内部（如图阴影部分）的任意一点，则z=x-2y的最小值为
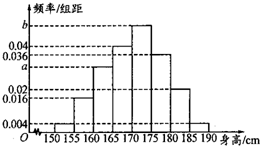某校要调查高中二年级男生的身高情况，现从全年级男生中随机抽取一个容量为100的样本．样本数据统计如表，对应的频率分布直方图如图所示．为了得到函数y=sin2x的图象，只需把函数y=cos2x的图象（ ）
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|