题目内容
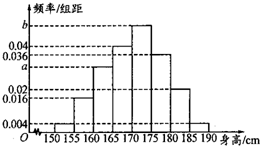某校要调查高中二年级男生的身高情况，现从全年级男生中随机抽取一个容量为100的样本．样本数据统计如表，对应的频率分布直方图如图所示．（1）求频率分布直方图中a，b的值；
（2）用样本估计总体，若该校高中二年级男生共有1000人，求该年级中男生身高不低于170cm的人数．
| 身高（单位：cm） | [150，155） | [155，160） | [160，165） | [165，170） | [170，175） | [175，180） | [180，185） | [185，190） |
| 人数 | 2 | 8 | 15 | 20 | 25 | 18 | 10 | 2 |
考点：频率分布直方图
专题：概率与统计
分析：（1）根据频率、频数与样本容量的关系，结合频率分布直方图中小矩形的高，求出a、b的值；
（2）求出该年级中男生身高不低于170cm的频率，计算对应的频数即可．
（2）求出该年级中男生身高不低于170cm的频率，计算对应的频数即可．
解答：
解：（1）身高在[160，165）的频率为
=0.15，
∴
=
=0.03，即a=0.03；
身高在[170，175）的频率为
=0.25，
∴
=
=0.05，即b=0.05；
（2）该年级中男生身高不低于170cm的频率为
0.25+0.036×5+0.02×5+0.004×5=0.55，
∴估计该年级中男生身高不低于170cm的人数是
1000×0.55=550．
| 15 |
| 100 |
∴
| 频率 |
| 组距 |
| 0.15 |
| 5 |
身高在[170，175）的频率为
| 25 |
| 100 |
∴
| 频率 |
| 组距 |
| 0.25 |
| 5 |
（2）该年级中男生身高不低于170cm的频率为
0.25+0.036×5+0.02×5+0.004×5=0.55，
∴估计该年级中男生身高不低于170cm的人数是
1000×0.55=550．
点评：本题考查了频率分布表与频率分布直方图的应用问题，是基础题目．
练习册系列答案
相关题目
已知⊙O：x2+y2=1，⊙M：x2+y2+4x-4y+4=0的位置关系是（ ）
| A、外离 | B、外切 | C、内含 | D、相交 |
已知实数x，y满足约束条件
，则z=x+3y的最大值等于（ ）
|
| A、9 | B、12 | C、27 | D、36 |
α，β表示不重合的两个平面，m，l表示不重合的两条直线．若α∩β=m，l?α，l?β，则“l∥m”是“l∥α且l∥β”的（ ）
| A、充分且不必要条件 |
| B、必要且不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
若a∈R，则a=2是（a-1）（a-2）=0的（ ）
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分又不必要条件 |
不等式（x-1）（2-x）≥0的解集是（ ）
| A、{x|1≤x≤2} |
| B、{x|x≥1或x≤2} |
| C、{x|1＜x＜2} |
| D、{x|x＞1或x＜2} |