题目内容
等比数列{an}的各项均为正数,且a1+3a2=
,a32=81a4a6
(1)求数列{an}的通项公式;
(2)设bn=2nlog3an,求数列{bn}的前n项和Sn.
| 2 |
| 3 |
(1)求数列{an}的通项公式;
(2)设bn=2nlog3an,求数列{bn}的前n项和Sn.
考点:数列的求和,数列递推式
专题:等差数列与等比数列
分析:(1)设等比数列{an}的公比为q(q>0),由已知列式求得等比数列的首项和公比,代入等比数列的通项公式得答案;
(2)把数列{an}的通项公式代入bn=2nlog3an,然后利用错位相减法求得数列{bn}的前n项和Sn.
(2)把数列{an}的通项公式代入bn=2nlog3an,然后利用错位相减法求得数列{bn}的前n项和Sn.
解答:
解:(1)设等比数列{an}的公比为q(q>0),
由a1+3a2=
,得3a1(1+3q)=2 ①,
又a32=81a4a6,得a32=81a3q4,即q=
.
把q=
代入①得,a1=
.
∴an=
;
(2)bn=2nlog3an=2nlog33-n=-n•2n,
∴Sn=-1•21-2•22-3•23-…-n•2n,
2Sn=-1•22-2•23-3•24-…-n•2n+1,
作差得:Sn=21+22+23+…+2n-n•2n+1
=
-n•2n+1=(1-n)•2n+1-2.
由a1+3a2=
| 2 |
| 3 |
又a32=81a4a6,得a32=81a3q4,即q=
| 1 |
| 3 |
把q=
| 1 |
| 3 |
| 1 |
| 3 |
∴an=
| 1 |
| 3n |
(2)bn=2nlog3an=2nlog33-n=-n•2n,
∴Sn=-1•21-2•22-3•23-…-n•2n,
2Sn=-1•22-2•23-3•24-…-n•2n+1,
作差得:Sn=21+22+23+…+2n-n•2n+1
=
| 2(1-2n) |
| 1-2 |
点评:本题考查了等比数列的通项公式,考查了错位相减法求数列的前n项和,是中档题.

练习册系列答案
相关题目
已知函数f(x)=
,若f(a)+f(1)=0,则实数a的值等于( )
|
| A、3 | B、1 | C、-3 | D、-1 |
已知集合A={x|-1≤x≤1},B={x|x2-2x≤0},则A∩(∁RB)=( )
| A、[-1,0) |
| B、[-1,0] |
| C、[0,1] |
| D、(-∞,1]∪[2,+∞) |
已知⊙O:x2+y2=1,⊙M:x2+y2+4x-4y+4=0的位置关系是( )
| A、外离 | B、外切 | C、内含 | D、相交 |
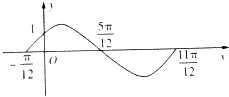 函数f1(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
函数f1(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<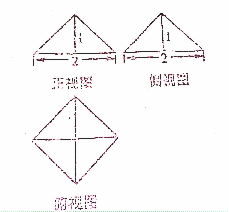 某几何体的三视图如图所示,其中正视图、侧视图均为斜边等于2的等腰直角三角形,俯视图是对角线为2的正方形,则该几何体的内切球的半径等于
某几何体的三视图如图所示,其中正视图、侧视图均为斜边等于2的等腰直角三角形,俯视图是对角线为2的正方形,则该几何体的内切球的半径等于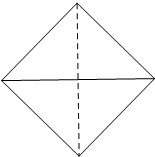 已知四面体S-ABC的所有棱长都相等,它的俯视图是一个边长为
已知四面体S-ABC的所有棱长都相等,它的俯视图是一个边长为