题目内容
已知tanα=m(m≠0),求出cosα和sinα.
考点:同角三角函数基本关系的运用
专题:三角函数的求值
分析:由tanα=m(m≠0),先切化弦,再利用平方关系,求出cosα,即可求出sinα.
解答:
解:∵tanα=m(m≠0),
∴
=m,
∴sinα=mcosα,
两边平方得sin2α=m2cos2α,
即1-cos2α=m2cos2α,
整理得(1+m2)cos2α=1;
∴cos2α=
,
①若α是第一象限或第四象限,则cosα=
=
;
∴sinα=mcosα=
;
②若α是第二象限或第三象限,则cosα=-
=-
;
∴sinα=mcosα=-
.
∴
| sinα |
| cosα |
∴sinα=mcosα,
两边平方得sin2α=m2cos2α,
即1-cos2α=m2cos2α,
整理得(1+m2)cos2α=1;
∴cos2α=
| 1 |
| 1+m2 |
①若α是第一象限或第四象限,则cosα=
|
| ||
| 1+m2 |
∴sinα=mcosα=
m•
| ||
| 1+m2 |
②若α是第二象限或第三象限,则cosα=-
|
| ||
| 1+m2 |
∴sinα=mcosα=-
m•
| ||
| 1+m2 |
点评:本题考查了同角的三角函数的运算关系,解题时应熟练地掌握同角三角函数的基本关系公式,注意要对角进行讨论.

练习册系列答案
相关题目
已知函数f(x)=
,若f(a)+f(1)=0,则实数a的值等于( )
|
| A、3 | B、1 | C、-3 | D、-1 |
已知⊙O:x2+y2=1,⊙M:x2+y2+4x-4y+4=0的位置关系是( )
| A、外离 | B、外切 | C、内含 | D、相交 |
α,β表示不重合的两个平面,m,l表示不重合的两条直线.若α∩β=m,l?α,l?β,则“l∥m”是“l∥α且l∥β”的( )
| A、充分且不必要条件 |
| B、必要且不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
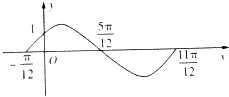 函数f1(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
函数f1(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<