题目内容
为了得到函数y=sin2x的图象,只需把函数y=cos2x的图象( )
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
考点:函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:由于y=sin2x=cos2(x-
),根据函数y=Asin(ωx+φ)的图象变换规律,得出结论.
| π |
| 4 |
解答:
解:由于函数y=sin2x=cos(
-2x)=cos(2x-
)=cos2(x-
),
故把y=cos2x的图象向右平移
个单位,即可得到函数y=sin2x的图象,
故选:B.
| π |
| 2 |
| π |
| 2 |
| π |
| 4 |
故把y=cos2x的图象向右平移
| π |
| 4 |
故选:B.
点评:本题主要考查诱导公式的应用,函数y=Asin(ωx+φ)的图象变换规律,属于中档题.

练习册系列答案
相关题目
已知⊙O:x2+y2=1,⊙M:x2+y2+4x-4y+4=0的位置关系是( )
| A、外离 | B、外切 | C、内含 | D、相交 |
α,β表示不重合的两个平面,m,l表示不重合的两条直线.若α∩β=m,l?α,l?β,则“l∥m”是“l∥α且l∥β”的( )
| A、充分且不必要条件 |
| B、必要且不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
若a∈R,则a=2是(a-1)(a-2)=0的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分又不必要条件 |
若一个等差数列首项为0,公差为2,则这个等差数列的前20项之和为( )
| A、360 | B、370 |
| C、380 | D、390 |
不等式(x-1)(2-x)≥0的解集是( )
| A、{x|1≤x≤2} |
| B、{x|x≥1或x≤2} |
| C、{x|1<x<2} |
| D、{x|x>1或x<2} |
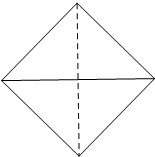 已知四面体S-ABC的所有棱长都相等,它的俯视图是一个边长为
已知四面体S-ABC的所有棱长都相等,它的俯视图是一个边长为