题目内容
已知双曲线C:
-
=1(a>0,b>0)的离心率为2,A,B为其左右顶点,点P为双曲线C在第一象限的任意一点,点O为坐标原点,若PA,PB,PO的斜率为k1,k2,k3,则m=k1k2k3的取值范围为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、(0,3
| ||||
B、(0,
| ||||
C、(0,
| ||||
| D、(0,8) |
考点:双曲线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:由已知条件推导出b=
a,k1k2=
•
=
=
=3,0<k3<
,由此能求出m=k1k2k3的取值范围.
| 3 |
| y |
| x+a |
| y |
| x-a |
| y2 |
| x2-a2 |
| b2 |
| a2 |
| 3 |
解答:
解:∵双曲线C:
-
=1(a>0,b>0)的离心率为2,
∴e=
=2,∴b=
=
a,
设P(x,y),∵点P为双曲线C在第一象限的任意一点,∴
-
=1,
∵A,B为双曲线C的左右顶点,点O为坐标原点,PA,PB,PO的斜率为k1,k2,k3,
∴k1k2=
•
=
=
=3,
又∵双曲线渐近线为y=±
x,∴0<k3<
,
∴0<m=k1k2k3<3
,
故选:A.
| x2 |
| a2 |
| y2 |
| b2 |
∴e=
| c |
| a |
| c2-a2 |
| 3 |
设P(x,y),∵点P为双曲线C在第一象限的任意一点,∴
| x2 |
| a2 |
| y2 |
| b2 |
∵A,B为双曲线C的左右顶点,点O为坐标原点,PA,PB,PO的斜率为k1,k2,k3,
∴k1k2=
| y |
| x+a |
| y |
| x-a |
| y2 |
| x2-a2 |
| b2 |
| a2 |
又∵双曲线渐近线为y=±
| 3 |
| 3 |
∴0<m=k1k2k3<3
| 3 |
故选:A.
点评:本题考查斜率乘积的取值范围的求法,是中档题,解题时要认真审题,要熟练掌握双曲线的简单性质.

练习册系列答案
相关题目
已知{an}是由正数组成的等比数列,Sn为其n项和.若a2a4=16,S3=7,则S4=( )
| A、15 | ||
| B、31 | ||
| C、63 | ||
D、
|
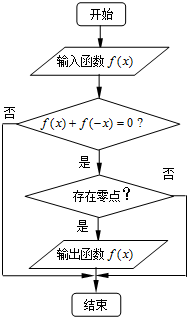 某流程如图所示,现输入四个函数,则可以输出的函数是( )
某流程如图所示,现输入四个函数,则可以输出的函数是( )| A、f(x)=x2 | ||
B、f(x)=
| ||
| C、f(x)=lnx+2x-6 | ||
| D、f(x)=x3 |
设α,β为两个不同的平面,m,n为两条不同的直线,且m?α,n?β,下列说法正确的是( )
| A、若m∥n,则α∥β |
| B、若m⊥β,则α⊥β |
| C、若m∥β,则α∥β |
| D、若α∥β,则m∥n |
已知数列{an},满足an=an-1-3,a2=3,则a9=( )
| A、18 | B、24 |
| C、-18 | D、-21 |
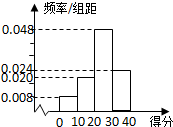 对甲、乙两名篮球运动员分别在100场比赛中的得分情况进行统计,做出甲的得分频率分布直方图如图,列出乙的得分统计表如下:
对甲、乙两名篮球运动员分别在100场比赛中的得分情况进行统计,做出甲的得分频率分布直方图如图,列出乙的得分统计表如下: