题目内容
已知
=(-3,4),若|
|=1,
⊥
,则
= .
| a |
| b |
| b |
| a |
| b |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:设
=(x,y),则由题意可得
,解得x、y的值,可得
的坐标.
| b |
|
| b |
解答:
解:∵
=(-3,4),|
|=1,
⊥
,设
=(x,y),则有
,
解得
,或
,
故答案为:(
,
)或(-
,-
).
| a |
| b |
| b |
| a |
| b |
|
解得
|
|
故答案为:(
| 4 |
| 5 |
| 3 |
| 5 |
| 4 |
| 5 |
| 3 |
| 5 |
点评:本题主要考查两个向量的数量积公式,两个向量垂直的性质,属于中档题.

练习册系列答案
相关题目
阅读如图所示的程序框图,运行相应的程序,输出的s值等于( )


| A、-3 | B、-21 | C、3 | D、21 |
已知双曲线C:
-
=1(a>0,b>0)的离心率为2,A,B为其左右顶点,点P为双曲线C在第一象限的任意一点,点O为坐标原点,若PA,PB,PO的斜率为k1,k2,k3,则m=k1k2k3的取值范围为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、(0,3
| ||||
B、(0,
| ||||
C、(0,
| ||||
| D、(0,8) |
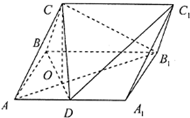 在三棱柱ABC-A1B1C1中,侧面ABBA1为矩形,AB=1,AA1=
在三棱柱ABC-A1B1C1中,侧面ABBA1为矩形,AB=1,AA1=
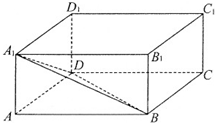 如图,长方体ABCD-A1B1C1D1,有一动点在此长方体内随机运动,则此动点在三棱锥A-A1BD内的概率为
如图,长方体ABCD-A1B1C1D1,有一动点在此长方体内随机运动,则此动点在三棱锥A-A1BD内的概率为