题目内容
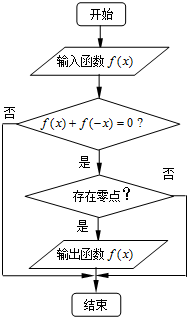 某流程如图所示,现输入四个函数,则可以输出的函数是( )
某流程如图所示,现输入四个函数,则可以输出的函数是( )| A、f(x)=x2 | ||
B、f(x)=
| ||
| C、f(x)=lnx+2x-6 | ||
| D、f(x)=x3 |
考点:程序框图
专题:算法和程序框图
分析:根据程序框图可知,第一个条件是判断啊何时能是否是奇函数,第二个条件判断函数是否有零点,根据条件分别进行判断即可.
解答:
解:第一个条件是判断啊何时能是否是奇函数,第二个条件判断函数是否有零点.
若f(x)=x2,不是奇函数,不满足条件.
若f(x)=
,是奇函数,但f(x)没有零点,不满足条件.
若f(x)=lnx+2x-6,是非奇非偶函数,不是奇函数,不满足条件,
若f(x)=x3,是奇函数满足第一个条件,由f(x)=x3=0,解得x=0,存在零点,满足第二个条件,
故输出函数为f(x)=x3,
故选:D
若f(x)=x2,不是奇函数,不满足条件.
若f(x)=
| 1 |
| x |
若f(x)=lnx+2x-6,是非奇非偶函数,不是奇函数,不满足条件,
若f(x)=x3,是奇函数满足第一个条件,由f(x)=x3=0,解得x=0,存在零点,满足第二个条件,
故输出函数为f(x)=x3,
故选:D
点评:本题主要考查程序框图的识别和判断,根据条件确定函数的奇偶性和函数是否存在零点是解决本题的关键.

练习册系列答案
相关题目
阅读如图所示的程序框图,运行相应的程序,输出的s值等于( )


| A、-3 | B、-21 | C、3 | D、21 |
如图是一个几何体的三视图,则该几何体的体积是( )


| A、3 | ||
B、
| ||
| C、1 | ||
D、
|
如图程序执行后输出的结果是S=( )


| A、3 | B、6 | C、10 | D、15 |
执行如图所示的程序框图,若输入n的值为7,则输出的s的值为( )


| A、22 | B、16 | C、15 | D、11 |
已知双曲线C:
-
=1(a>0,b>0)的离心率为2,A,B为其左右顶点,点P为双曲线C在第一象限的任意一点,点O为坐标原点,若PA,PB,PO的斜率为k1,k2,k3,则m=k1k2k3的取值范围为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、(0,3
| ||||
B、(0,
| ||||
C、(0,
| ||||
| D、(0,8) |
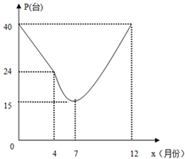 由于国家重点扶持节能环保产业,某种节能产品的市场销售回暖.某经销商销售这种产品,年初与生产厂家签订进货合同,约定一年内进价为0.1万元/台.一年后,实际月销售量P(台)与月次x之间存在如图所示函数关系(4月到12月近似符合二次函数关系).
由于国家重点扶持节能环保产业,某种节能产品的市场销售回暖.某经销商销售这种产品,年初与生产厂家签订进货合同,约定一年内进价为0.1万元/台.一年后,实际月销售量P(台)与月次x之间存在如图所示函数关系(4月到12月近似符合二次函数关系).