题目内容
设α,β为两个不同的平面,m,n为两条不同的直线,且m?α,n?β,下列说法正确的是( )
| A、若m∥n,则α∥β |
| B、若m⊥β,则α⊥β |
| C、若m∥β,则α∥β |
| D、若α∥β,则m∥n |
考点:空间中直线与平面之间的位置关系
专题:探究型,空间位置关系与距离
分析:A,C,利用面面平行的判定定理,可知不正确;B,根据面面垂直的判定定理,可得α⊥β;D,α∥β,若m,n是第三平面与α,β的两条交线时,m∥n.
解答:
解:对于A,利用面面平行的判定定理,可知不正确;
对于B,若m⊥β,m?α,n?β,根据面面垂直的判定定理,可得α⊥β,故正确;
对于C,m∥β,利用面面平行的判定定理,可知不正确;
对于D,α∥β,若m,n是第三平面与α,β的两条交线时,m∥n,故不正确;
故选:B.
对于B,若m⊥β,m?α,n?β,根据面面垂直的判定定理,可得α⊥β,故正确;
对于C,m∥β,利用面面平行的判定定理,可知不正确;
对于D,α∥β,若m,n是第三平面与α,β的两条交线时,m∥n,故不正确;
故选:B.
点评:本题考查了空间中平面与平面的位置关系,主要根据面面位置关系进行分类判断,考查了空间想象能力.

练习册系列答案
相关题目
各项均为正数的数列{an}的前n项和Sn,且3Sn=anan+1,则
a2k=( )
| n |
 |
| i=1 |
A、
| ||
B、
| ||
C、
| ||
D、
|
如图程序执行后输出的结果是S=( )


| A、3 | B、6 | C、10 | D、15 |
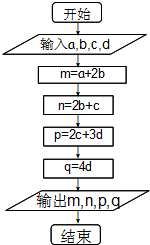 为确保信息安全,信息需加密传输,发送方由明文→密文(加密),接收方由密文→明文(解密),已知加密规则如图所示,例如明文1,2,3,4,对应密文5,7,18,16.当对方收到密文14,9,23,28时,则解密得到的明文为( )
为确保信息安全,信息需加密传输,发送方由明文→密文(加密),接收方由密文→明文(解密),已知加密规则如图所示,例如明文1,2,3,4,对应密文5,7,18,16.当对方收到密文14,9,23,28时,则解密得到的明文为( )| A、4,6,1,7 |
| B、6,4,1,7 |
| C、1,6,4,7 |
| D、7,6,1,4 |
已知双曲线C:
-
=1(a>0,b>0)的离心率为2,A,B为其左右顶点,点P为双曲线C在第一象限的任意一点,点O为坐标原点,若PA,PB,PO的斜率为k1,k2,k3,则m=k1k2k3的取值范围为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、(0,3
| ||||
B、(0,
| ||||
C、(0,
| ||||
| D、(0,8) |
阅读如图程序框图,输出的结果i的值为( )
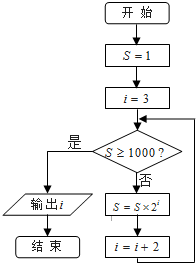

| A、5 | B、6 | C、7 | D、9 |
 运行如图所示的程序框图,当输入实数x的值为-1时,输出的函数值为2;当输入实数x的值为3时,输出的函数值为7.
运行如图所示的程序框图,当输入实数x的值为-1时,输出的函数值为2;当输入实数x的值为3时,输出的函数值为7.