题目内容
已知数列{an},满足an=an-1-3,a2=3,则a9=( )
| A、18 | B、24 |
| C、-18 | D、-21 |
考点:等差数列的通项公式
专题:等差数列与等比数列
分析:由已知条件推导出数列{an}是公差d=-3的等差数列,再由a9=a2+7d能求出结果.
解答:
解:∵数列{an},满足an=an-1-3,
∴an-an-1=-3,
∴数列{an}是公差d=-3的等差数列,
∵a2=3,∴a9=a2+7d=3+7×(-3)=-18.
故选:C.
∴an-an-1=-3,
∴数列{an}是公差d=-3的等差数列,
∵a2=3,∴a9=a2+7d=3+7×(-3)=-18.
故选:C.
点评:本题考查数列中的第9项的求法,是基础题,解题时要熟练掌握等差数列的通项公式的灵活运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
如图是一个几何体的三视图,则该几何体的体积是( )


| A、3 | ||
B、
| ||
| C、1 | ||
D、
|
执行如图所示的程序框图,若输入n的值为7,则输出的s的值为( )


| A、22 | B、16 | C、15 | D、11 |
已知双曲线C:
-
=1(a>0,b>0)的离心率为2,A,B为其左右顶点,点P为双曲线C在第一象限的任意一点,点O为坐标原点,若PA,PB,PO的斜率为k1,k2,k3,则m=k1k2k3的取值范围为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、(0,3
| ||||
B、(0,
| ||||
C、(0,
| ||||
| D、(0,8) |
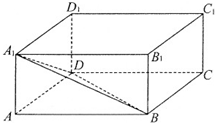 如图,长方体ABCD-A1B1C1D1,有一动点在此长方体内随机运动,则此动点在三棱锥A-A1BD内的概率为
如图,长方体ABCD-A1B1C1D1,有一动点在此长方体内随机运动,则此动点在三棱锥A-A1BD内的概率为 如图,在Rt△AOB中,∠OAB=
如图,在Rt△AOB中,∠OAB=