题目内容
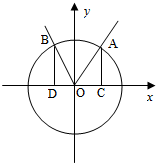 如图,在平面直角坐标系xOy中,点A(x1,y1),B(x2,y2)在单位平面上,∠xOA=α,∠AOB=
如图,在平面直角坐标系xOy中,点A(x1,y1),B(x2,y2)在单位平面上,∠xOA=α,∠AOB=| π |
| 3 |
| π |
| 6 |
| π |
| 2 |
(Ⅰ)若cos(α+
| π |
| 3 |
| ||
| 14 |
(Ⅱ)过点A,B分别做x轴的垂线,垂足为C、D,记△AOC的面积为S1,△BOD的面积为S2.设f(α)=S1+S2,求函数f(α)的最大值.
考点:任意角的三角函数的定义,三角函数中的恒等变换应用
专题:三角函数的求值
分析:(Ⅰ)由三角函数的定义有x1=cosα ,x2=cos(α+
),由条件求得sin(α+
)=
,再根据x1=
cosα=cos[(α+
)-
],利用两角差的余弦公式求得结果.
(Ⅱ)由y1=sinα,得S1=x1y1=
cosαsinα=
sin2α,再求得y2=sin(α+
),可得S2=-
x2•y2=-
sin(2α+
),可得f(α)=S1+S2=
sin2α-
sin(2α+
),化简为
sin(2α-
),根据α∈(
,
),利用正弦函数的定义域和值域求得函数f(α)的最大值.
| π |
| 3 |
| π |
| 3 |
3
| ||
| 14 |
cosα=cos[(α+
| π |
| 3 |
| π |
| 3 |
(Ⅱ)由y1=sinα,得S1=x1y1=
| 1 |
| 2 |
| 1 |
| 4 |
| π |
| 3 |
| 1 |
| 2 |
| 1 |
| 4 |
sin(2α+
| 2π |
| 3 |
| 1 |
| 4 |
| 1 |
| 4 |
| 2π |
| 3 |
| ||
| 4 |
| π |
| 6 |
| π |
| 6 |
| π |
| 2 |
解答:
解:(Ⅰ)由三角函数的定义有x1=cosα ,x2=cos(α+
),
∵cos(α+
)=-
,α∈(
,
),∴sin(α+
)=
,
∴x1=cosα=cos[(α+
)-
]=cos(α+
)cos
+sin(α+
)sin
,
∴x1=
.
(Ⅱ)由y1=sinα,得S1=x1y1=
cosαsinα=
sin2α.
又由α∈(
,
) ,得α+
∈(
,
),于是y2=sin(α+
),
∴S2=-
x2y2=-
cos(α+
)sin(α+
)=-
sin(2α+
),
∴f(α)=S1+S2=
sin2α-
sin(2α+
)
=
sin2α-
(sin2αcos
+cos2αsin
)
=
sin2α-
cos2α=
(
sin2α-
cos2α)=
sin(2α-
),
由α∈(
,
) ,可得2α-
∈(
,
),于是当2α-
=
,
即α=
时,f(α)max=
.
| π |
| 3 |
∵cos(α+
| π |
| 3 |
| ||
| 14 |
| π |
| 6 |
| π |
| 2 |
| π |
| 3 |
3
| ||
| 14 |
∴x1=cosα=cos[(α+
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
∴x1=
2
| ||
| 7 |
(Ⅱ)由y1=sinα,得S1=x1y1=
| 1 |
| 2 |
| 1 |
| 4 |
又由α∈(
| π |
| 6 |
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
| 5π |
| 6 |
| π |
| 3 |
∴S2=-
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 3 |
| π |
| 3 |
| 1 |
| 4 |
| 2π |
| 3 |
∴f(α)=S1+S2=
| 1 |
| 4 |
| 1 |
| 4 |
| 2π |
| 3 |
=
| 1 |
| 4 |
| 1 |
| 4 |
| 2π |
| 3 |
| 2π |
| 3 |
=
| 3 |
| 8 |
| ||
| 8 |
| ||
| 4 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 4 |
| π |
| 6 |
由α∈(
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
| π |
| 6 |
| π |
| 2 |
即α=
| π |
| 3 |
| ||
| 4 |
点评:本题主要考查任意角的三角函数的定义,同角三角函数的基本关系,三角函数的恒等变换,属于中档题.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
设z∈C,若z2为纯虚数,则z在复平面上的对应点落在( )
| A、实轴上 |
| B、虚轴上 |
| C、直线y=±x(x≠0)上 |
| D、以上都不对 |

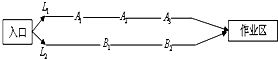 某煤矿发生透水事故时,作业区有若干人员被困.救援队从入口进入之后有L1,L2两条巷道通往作业区(如图),L1巷道有A1,A2,A3三个易堵塞点,各点被堵塞的概率都是
某煤矿发生透水事故时,作业区有若干人员被困.救援队从入口进入之后有L1,L2两条巷道通往作业区(如图),L1巷道有A1,A2,A3三个易堵塞点,各点被堵塞的概率都是