题目内容
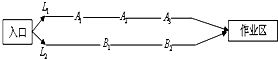 某煤矿发生透水事故时,作业区有若干人员被困.救援队从入口进入之后有L1,L2两条巷道通往作业区(如图),L1巷道有A1,A2,A3三个易堵塞点,各点被堵塞的概率都是
某煤矿发生透水事故时,作业区有若干人员被困.救援队从入口进入之后有L1,L2两条巷道通往作业区(如图),L1巷道有A1,A2,A3三个易堵塞点,各点被堵塞的概率都是| 1 |
| 2 |
| 3 |
| 4 |
| 3 |
| 5 |
(Ⅰ)求L1巷道中,三个易堵塞点最多有一个被堵塞的概率;
(Ⅱ)若L2巷道中堵塞点个数为X,求X的分布列及数学期望EX,并按照“平均堵塞点少的巷道是较好的抢险路线“的标准,请你帮助救援队选择一条抢险路线,并说明理由.
考点:离散型随机变量的期望与方差,互斥事件的概率加法公式
专题:综合题,概率与统计
分析:(Ⅰ)利用互独立事件的概率计算公式即可得出;
(Ⅱ)比较走两条路的数学期望的大小,即可得出要选择的路线.
(Ⅱ)比较走两条路的数学期望的大小,即可得出要选择的路线.
解答:
解:(Ⅰ)设”L1巷道中,三个易堵塞点最多有一个被堵塞”为事件A
则P(A)=
×(
)3+
×
×(
)2=
(Ⅱ)依题意,X的可能取值为0,1,2
P(X=0)=(1-
)×(1-
)=
P(X=1)=
×(1-
)+(1-
)×
=
P(X=2)=
×
=
所以,随机变量X的分布列为:
EX=0×
+1×
+2×
=
设L1巷道中堵塞点个数为Y,则Y的可能取值为0,1,2,3,
P(Y=0)=
×(
)3=
,
P(Y=1)=
×
×(
)2=
,
P(Y=2)=
×(
)2×
=
,
P(Y=3)=
×(
)3=
,
所以,随机变量Y的分布列为:
EY=0×
+1×
+2×
+3×
=
.
因为EX<EY,所以选择L2巷道为抢险路线为好.
则P(A)=
| C | 0 3 |
| 1 |
| 2 |
| C | 1 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(Ⅱ)依题意,X的可能取值为0,1,2
P(X=0)=(1-
| 3 |
| 4 |
| 3 |
| 5 |
| 1 |
| 10 |
| 3 |
| 4 |
| 3 |
| 5 |
| 3 |
| 4 |
| 3 |
| 5 |
| 9 |
| 20 |
| 3 |
| 4 |
| 3 |
| 5 |
| 9 |
| 20 |
所以,随机变量X的分布列为:
| X | 0 | 1 | 2 | ||||||
| P |
|
|
|
| 1 |
| 10 |
| 9 |
| 20 |
| 9 |
| 20 |
| 27 |
| 20 |
设L1巷道中堵塞点个数为Y,则Y的可能取值为0,1,2,3,
P(Y=0)=
| C | 0 3 |
| 1 |
| 2 |
| 1 |
| 8 |
P(Y=1)=
| C | 1 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 8 |
P(Y=2)=
| C | 2 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 8 |
P(Y=3)=
| C | 3 3 |
| 1 |
| 2 |
| 1 |
| 8 |
所以,随机变量Y的分布列为:
| Y | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
| 1 |
| 8 |
| 3 |
| 8 |
| 3 |
| 8 |
| 1 |
| 8 |
| 3 |
| 2 |
因为EX<EY,所以选择L2巷道为抢险路线为好.
点评:熟练掌握二项分布列、相互独立事件的概率计算公式及离散型随机变量的期望计算公式及其意义是解题的关键.

练习册系列答案
相关题目
若1和a的等差中项是2,则a的值为( )
| A、4 | B、3 | C、1 | D、-4 |
 在如图所示的几何体中,四边形ABCD是等腰梯形,AB∥CD,∠DAB=60°,FC⊥平面ABCD,AE⊥BD,CB=CD=CF.
在如图所示的几何体中,四边形ABCD是等腰梯形,AB∥CD,∠DAB=60°,FC⊥平面ABCD,AE⊥BD,CB=CD=CF.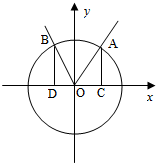 如图,在平面直角坐标系xOy中,点A(x1,y1),B(x2,y2)在单位平面上,∠xOA=α,∠AOB=
如图,在平面直角坐标系xOy中,点A(x1,y1),B(x2,y2)在单位平面上,∠xOA=α,∠AOB=