题目内容
某合资企业招聘夫学生时加试英语听力,待测试的小组中有男、女生共10人(其中女生人数多于男生人数),若从中随机选2人,其中恰为一男一女的概率为
.
(Ⅰ)求该小组中女生的人数:
(Ⅱ)若该小组中每个女生通过测试的概率均为
,每个男生通过测试的概率均为
;现对该小组中女生甲、女生乙和男生丙、男生丁4人进行测试,记这4人中通过测试的人数为随机变量X.求X的分布列和数学期望.
| 8 |
| 15 |
(Ⅰ)求该小组中女生的人数:
(Ⅱ)若该小组中每个女生通过测试的概率均为
| 3 |
| 4 |
| 2 |
| 3 |
考点:离散型随机变量的期望与方差,等可能事件的概率
专题:综合题,概率与统计
分析:(I)设出该小组中有n个女生,根据古典概型的概率公式得到比值,等于恰为一男一女的概率,解出关于n的方程.
(Ⅱ)由题意知X的取值为0,1,2,3,4,结合变量对应的事件,和独立重复试验的概率公式,得到变量对应的概率,写出分布列,求出期望值.
(Ⅱ)由题意知X的取值为0,1,2,3,4,结合变量对应的事件,和独立重复试验的概率公式,得到变量对应的概率,写出分布列,求出期望值.
解答:
解:(Ⅰ)设该小组中有n个女生,
由题意,得
=
,
解得n=6或n=4(舍),
所以该小组有6名女生;
(Ⅱ)由题意,X的取值为0,1,2,3,4
P(X=0)=(
)2×(
)2=
,
P(X=1)=
×
×
×(
)2+
×(
)2×
×
=
,
P(X=2)=(
)2×(
)2+(
)2×
×
×
×
+(
)2×(
)2=
,
P(X=3)=
×
×
×(
)2+
×(
)2×
×
=
,
P(X=4)=(
)2×(
)2=
.
所以X的分布列为:
所以EX=0×
+1×
+2×
+3×
+4×
=
由题意,得
| ||||
|
| 8 |
| 15 |
解得n=6或n=4(舍),
所以该小组有6名女生;
(Ⅱ)由题意,X的取值为0,1,2,3,4
P(X=0)=(
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 144 |
P(X=1)=
| C | 1 2 |
| 3 |
| 4 |
| 1 |
| 4 |
| 1 |
| 3 |
| C | 1 2 |
| 1 |
| 4 |
| 2 |
| 3 |
| 1 |
| 3 |
| 5 |
| 72 |
P(X=2)=(
| 3 |
| 4 |
| 1 |
| 3 |
| C | 1 2 |
| 3 |
| 4 |
| 2 |
| 3 |
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 4 |
| 2 |
| 3 |
| 37 |
| 144 |
P(X=3)=
| C | 1 2 |
| 3 |
| 4 |
| 1 |
| 4 |
| 2 |
| 3 |
| C | 1 2 |
| 3 |
| 4 |
| 2 |
| 3 |
| 1 |
| 3 |
| 5 |
| 12 |
P(X=4)=(
| 3 |
| 4 |
| 2 |
| 3 |
| 1 |
| 4 |
所以X的分布列为:
| X | 0 | 1 | 2 | 3 | 4 | ||||||||||
| P |
|
|
|
|
|
| 1 |
| 144 |
| 5 |
| 72 |
| 37 |
| 144 |
| 5 |
| 12 |
| 1 |
| 4 |
| 17 |
| 6 |
点评:本题考查离散型随机变量的分布列和期望,考查古典概型的概率公式,考查独立重复试验的概率公式,考查利用概率与统计的知识解决实际问题.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
若
=(x,3),
=(3,1)且
∥
,则x的值是( )
| a |
| b |
| a |
| b |
| A、-9 | B、-1 | C、1 | D、9 |
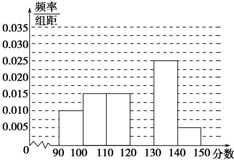 某校从参加高三模拟考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六组[90,100),[100,110),…,[140,150]后得到如下部分频率分布直方图,观察图形的信息,回答下列问题:
某校从参加高三模拟考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六组[90,100),[100,110),…,[140,150]后得到如下部分频率分布直方图,观察图形的信息,回答下列问题: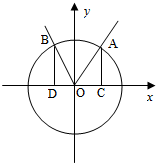 如图,在平面直角坐标系xOy中,点A(x1,y1),B(x2,y2)在单位平面上,∠xOA=α,∠AOB=
如图,在平面直角坐标系xOy中,点A(x1,y1),B(x2,y2)在单位平面上,∠xOA=α,∠AOB=