题目内容
设z∈C，若z2为纯虚数，则z在复平面上的对应点落在（ ）
| A、实轴上 |
| B、虚轴上 |
| C、直线y=±x（x≠0）上 |
| D、以上都不对 |
考点：复数的代数表示法及其几何意义
专题：数系的扩充和复数
分析：设出复数z，利用z2为纯虚数，推出复数实部与虚部的关系，判断z在复平面上的对应点落在位置即可．
解答：
解：设复数z=a+bi，
∴z2=a2-b2+2abi，
z2为纯虚数，
∴a2-b2=0且ab≠0，
即a=±b且ab≠0，
∴z在复平面上的对应点落在直线y=±x（x≠0）上．
故选：C．
∴z2=a2-b2+2abi，
z2为纯虚数，
∴a2-b2=0且ab≠0，
即a=±b且ab≠0，
∴z在复平面上的对应点落在直线y=±x（x≠0）上．
故选：C．
点评：本题考查复数的基本概念以及复数的几何意义，考查计算能力．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
执行如图所示的程序框图，则输出的a为（ ）
| A、20 | B、14 | C、10 | D、7 |
给出下列等式
①
=
②
=a
③{y|y=-x2+x-1，x≥1}∩{x|x=
-2，m≥0}={-1}
④{x||1-2x|＜5}∪{x|6-x-x2＞0}={x|-
＞0}
则上述等式成立的是（ ）
①
log51-log5
|
| 1-2log52 |
②
| a6 | ||||
|
| 6 |
| 5 |
③{y|y=-x2+x-1，x≥1}∩{x|x=
| m+1 |
④{x||1-2x|＜5}∪{x|6-x-x2＞0}={x|-
| x+3 |
| x-3 |
则上述等式成立的是（ ）
| A、①③ | B、①② | C、①④ | D、①③④ |
若向量
=（1，2），
=（4，5），则
=（ ）
| BA |
| CA |
| BC |
| A、（5，7） |
| B、（-3，-3） |
| C、（3，3） |
| D、（-5，-7） |
若1和a的等差中项是2，则a的值为（ ）
| A、4 | B、3 | C、1 | D、-4 |
若
=（x，3），
=（3，1）且
∥
，则x的值是（ ）
| a |
| b |
| a |
| b |
| A、-9 | B、-1 | C、1 | D、9 |
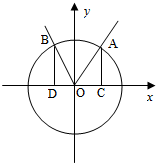如图，在平面直角坐标系xOy中，点A（x1，y1），B（x2，y2）在单位平面上，∠xOA=α，∠AOB=