题目内容
命题p：方程
+
=1表示焦点在y轴上的椭圆，命题q：关于x的不等式4x2-4mx+（4m-3）≥0在R上恒成立，若p∨q为真，?p为真，求实数m的取值范围．
| x2 |
| 2 |
| y2 |
| m |
考点：复合命题的真假
专题：简易逻辑
分析：先求出命题p，q为真命题时m的范围，利用复合命题的真假与简单命题真假的关系由条件“p∨q为真，?p为真”得出p假q真，求出m的范围．
解答：
解：命题p为真命题时，m＞2
命题q为真命题时，△=（-4m）2-16（4m-3）≤0
∴1≤m≤3，
∵p∨q为真，?p为真，
∴p假q真，
，
∴1≤m≤2
命题q为真命题时，△=（-4m）2-16（4m-3）≤0
∴1≤m≤3，
∵p∨q为真，?p为真，
∴p假q真，
|
∴1≤m≤2
点评：本题考查复合命题的真假与构成其简单命题真假的关系，解决此类问题的关键是先求出简单命题为真命题时参数的范围，属于易错题．
练习册系列答案
名校课堂系列答案
相关题目
执行如图所示的程序框图，则输出的a为（ ）
| A、20 | B、14 | C、10 | D、7 |
若
=（x，3），
=（3，1）且
∥
，则x的值是（ ）
| a |
| b |
| a |
| b |
| A、-9 | B、-1 | C、1 | D、9 |
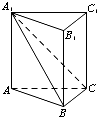如图，在直三棱柱ABC-A1B1C1中，平面A1BC⊥侧面A1ABB1．
在如图所示的几何体中，四边形ABCD是等腰梯形，AB∥CD，∠DAB=60°，FC⊥平面ABCD，AE⊥BD，CB=CD=CF．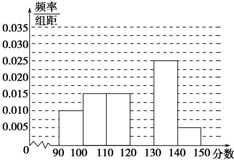
某校从参加高三模拟考试的学生中随机抽取60名学生，将其数学成绩（均为整数）分成六组[90，100），[100，110），…，[140，150]后得到如下部分频率分布直方图，观察图形的信息，回答下列问题：
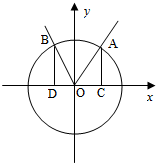如图，在平面直角坐标系xOy中，点A（x1，y1），B（x2，y2）在单位平面上，∠xOA=α，∠AOB=