题目内容
若轴截面是正方形的圆柱的上、下底面圆周均位于一个球面上,且球与圆柱的体积分别为V1和V2,则V1:V2的值为 .
考点:旋转体(圆柱、圆锥、圆台)
专题:函数的性质及应用
分析:因为圆柱截面为正方形,则圆柱高与底面直径长相等,设为2R,又上下底面圆周均在同一球面上,进而求出球面半径,分别计算出球与圆柱的体积分别为V1和V2,可得答案.
解答:
解:∵圆柱截面为正方形,则圆柱高与底面直径长相等,设为2R,
则球面半径为为
=
R.
∴V1:V2=
π(
R)3:2πR3=
,
故答案为:
则球面半径为为
| ||
| 2 |
| 2 |
∴V1:V2=
| 4 |
| 3 |
| 2 |
| 4 |
| 3 |
| 2 |
故答案为:
| 4 |
| 3 |
| 2 |
点评:本题考查的知识点是旋转体,熟练掌握圆柱和球的体积公式,是解答的关键.

练习册系列答案
相关题目
利用计算机在区间(0,1)上产生两个随机数a和b,则函数y=x+
-2
有零点的概率为( )
| b |
| x |
| a |
A、
| ||
B、
| ||
C、
| ||
| D、1 |
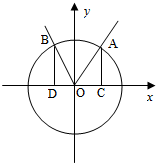 如图,在平面直角坐标系xOy中,点A(x1,y1),B(x2,y2)在单位平面上,∠xOA=α,∠AOB=
如图,在平面直角坐标系xOy中,点A(x1,y1),B(x2,y2)在单位平面上,∠xOA=α,∠AOB=