题目内容
已知椭圆C:
+
=1(a>0,b>0)的离心率与双曲线
-
=1的一条渐近线的斜率相等,以原点为圆心,椭圆的短半轴长为半径的圆与直线sinα•x+cosα•y-1=0相切(α为常数).
(1)求椭圆C的方程;
(2)若过点M(3,0)的直线与椭圆C相交于A,B两点,设P为椭圆上一点,且满足
+
=t
(O为坐标原点),当|
-
|<
时,求实数t取值范围.
| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| 4 |
| y2 |
| 3 |
(1)求椭圆C的方程;
(2)若过点M(3,0)的直线与椭圆C相交于A,B两点,设P为椭圆上一点,且满足
| OA |
| OB |
| OP |
| PB |
| PA |
| 3 |
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)根据双曲线
-
=1的一渐近线斜率值,确定椭圆的离心率,结合椭圆的短半轴长为半径的圆与直线sinα•x+cosα•y-1=0相切,求出椭圆的几何量,即可求椭圆C的方程;
(2)AB方程为y=k(x-3),代入椭圆方程,利用
+
=t
,确定P的坐标,代入椭圆方程得36k2=t2(1+4k2),由|AB|<
,即可求实数t取值范围.
| x2 |
| 4 |
| y2 |
| 3 |
(2)AB方程为y=k(x-3),代入椭圆方程,利用
| OA |
| OB |
| OP |
| 3 |
解答:
解:(1)由题意知双曲线
-
=1的一渐近线斜率值为
,
所以e=
=
,所以e2=
=
=
,所以a2=4b2,
因为b=
=1,所以a2=4,b2=1.
故椭圆C的方程为
+y2=1???????(5分)
(2)设A(x1,y1),B(x2,y2),P(x,y),AB方程为y=k(x-3)?
由
?整理得(1+4k2)x2-24k2x+36k2-4=0.
由△=(24k2)2-4(1+4k2)•(36k2-4)>0,
解得k2<
.x1+x2=
,x1•x2=
…(7分)
所以
+
=(x1+x2,y1+y2)=t(x,y)
则x=
(x1+x2)=
,y=
(y1+y2)=
,
由点P在椭圆上,代入椭圆方程得36k2=t2(1+4k2)①…(9分)
又由|AB|<
,即(1+k2)[(x1+x2)2-4x1•x2]<3,
将x1+x2=
,x1•x2=
,
代入得(8k2-1)•(16k2+13)>0
则8k2-1>0,k2>
,
所以
>k2>
②…(11分)
由①,得t2=
,联立②,解得3<t2<4
所以
<t<2或-2<t<-
…(13分)
| x2 |
| 4 |
| y2 |
| 3 |
| ||
| 2 |
所以e=
| c |
| a |
| ||
| 2 |
| c2 |
| a2 |
| a2-b2 |
| a2 |
| 3 |
| 4 |
因为b=
| 1 | ||
|
故椭圆C的方程为
| x2 |
| 4 |
(2)设A(x1,y1),B(x2,y2),P(x,y),AB方程为y=k(x-3)?
由
|
由△=(24k2)2-4(1+4k2)•(36k2-4)>0,
解得k2<
| 1 |
| 5 |
| 24k2 |
| 1+4k2 |
| 36k2-4 |
| 1+4k2 |
所以
| OA |
| OB |
则x=
| 1 |
| t |
| 24k2 |
| t(1+4k2) |
| 1 |
| t |
| -6k |
| t(1+4k2) |
由点P在椭圆上,代入椭圆方程得36k2=t2(1+4k2)①…(9分)
又由|AB|<
| 3 |
将x1+x2=
| 24k2 |
| 1+4k2 |
| 36k2-4 |
| 1+4k2 |
代入得(8k2-1)•(16k2+13)>0
则8k2-1>0,k2>
| 1 |
| 8 |
所以
| 1 |
| 5 |
| 1 |
| 8 |
由①,得t2=
| 36k2 |
| 1+4k2 |
所以
| 3 |
| 3 |
点评:本题考查直线与圆锥曲线的综合问题,考查椭圆的方程与性质,利用直线与椭圆联立,进而利用韦达定理是解题的关键.

练习册系列答案
相关题目
在复平面内,复数z=(1+2i)(1-i)对应的点位于( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
若{an}为等差数列,Sn是其前n项和,且S13=
π,则tana7的值为( )
| 13 |
| 4 |
| A、-1 | ||||
B、-
| ||||
C、±
| ||||
| D、1 |
已知条件p:α是两条直线的夹角,条件q:α是第一象限的角.则“条件p”是“条件q”的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
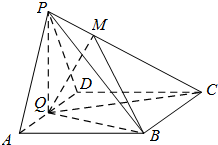 如图在四棱锥P-ABCD中,底面ABCD是菱形,∠BAD=60°,平面PAD⊥平面ABCD,PA=PD=AD=2,Q为AD的中点,M是棱PC上一点,且PM=
如图在四棱锥P-ABCD中,底面ABCD是菱形,∠BAD=60°,平面PAD⊥平面ABCD,PA=PD=AD=2,Q为AD的中点,M是棱PC上一点,且PM=