Question

3．在矩形ABCD中，AB=2AD=2$\sqrt{2}$，M为DC的中点，将△ADM沿AM折起，使得平面ADM⊥平面ABCM；
（1）求证：AD⊥BM
（2）若点E是线段DB上的一点，问点E在何位置时，二面角E-AM-D的余弦值为$\frac{\sqrt{5}}{5}$．

Answer 1

分析 （1）利用勾股定理证明BM⊥AM，结合面面垂直的性质得出BM⊥平面ADM，从而得出BM⊥AD；
（2）以AM中点O为原点建立空间直角坐标系，设$\overrightarrow{BE}=λ\overrightarrow{BD}$，求出两平面的法向量$\overrightarrow{m}，\overrightarrow{n}$，令|cos＜$\overrightarrow{m}，\overrightarrow{n}$＞|=$\frac{\sqrt{5}}{5}$解出λ即可得出E点位置．

解答 （1）证明：∵长方形ABCD中，AB=2$\sqrt{2}$，AD=$\sqrt{2}$，M为DC的中点，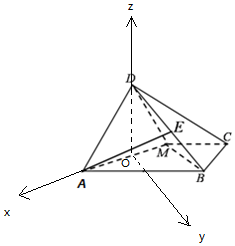
∴AM=BM=2，∴AM²+BM²=AB²，
∴BM⊥AM，
∵面ADM⊥面ABCM，平面ADM∩平面ABCM=AM，BM?平面ABCM，
∴BM⊥面ADM，
∵AD?面ADM，
∴BM⊥AD．
（2）解：以AM中点O为原点，OA为x轴，OD为z轴，建立空间直角坐标系O-xyz，
则A（1，0，0），B（-1，2，0），M（-1，0，0），D（0，0，1），
∴$\overrightarrow{MA}$=（2，0，0），$\overrightarrow{AB}$=（-2，2，0），$\overrightarrow{BD}$=（1，-2，1），
设$\overrightarrow{BE}=λ\overrightarrow{BD}$=（λ，-2λ，λ），则$\overrightarrow{AE}$=$\overrightarrow{AB}+$$\overrightarrow{BE}$=（λ-2，2-2λ，λ），
设平面AME的法向量为$\overrightarrow{m}$=（x，y，z），则$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{MA}=0}\\{\overrightarrow{m}•\overrightarrow{AE}=0}\end{array}\right.$，
∴$\left\{\begin{array}{l}{2x=0}\\{（λ-2）x+（2-2λ）y+λz=0}\end{array}\right.$，令y=1得$\overrightarrow{m}$=（0，1，2-$\frac{2}{λ}$）．
又BM⊥平面ADM，∴$\overrightarrow{n}$=（0，1，0）为平面ADM的一个法向量．
∴cos＜$\overrightarrow{m}，\overrightarrow{n}$＞=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}||\overrightarrow{n}|}$=$\frac{1}{\sqrt{1+（2-\frac{2}{λ}）^{2}}}$，
∵二面角E-AM-D的余弦值为$\frac{\sqrt{5}}{5}$，∴$\frac{1}{\sqrt{1+（2-\frac{2}{λ}）^{2}}}$=$\frac{\sqrt{5}}{5}$．
解得λ=$\frac{1}{2}$．
∴E为BD的中点．

点评 本题考查了线面垂直的判定，空间向量与空间角的计算，属于中档题．