题目内容
14.根据如表样本数据| x | 3 | 4 | 5 | 6 |
| y | 2.5 | t | 4 | 4.5 |
| A. | 2.6 | B. | 2.8 | C. | 2.9 | D. | 3 |
分析 根据已知表中数据,可计算出数据中心点($\overline{x}$,$\overline{y}$)的坐标,根据数据中心点一定在回归直线上,将($\overline{x}$,$\overline{y}$)的坐标代入回归直线方程y=0.7x+0.35,解方程可得m的值.
解答 解:由已知中的数据可得:$\overline{x}$=(3+4+5+6)÷4=4.5,$\overline{y}$=(2.5+t+4+4.5)÷4=$\frac{11+t}{4}$,
∵数据中心点($\overline{x}$,$\overline{y}$)一定在回归直线上,
∴$\frac{11+t}{4}$=0.7×4.5+0.35,
解得t=3,
故选:D.
点评 本题考查的知识点是线性回归方程,其中数据中心点($\overline{x}$,$\overline{y}$)一定在回归直线上是解答本题的关键.

练习册系列答案
相关题目
4.如图,某港口一天的水深变化曲线近似满足函数y=Asin$\frac{π}{6}$t+k,则水深从最小值变化到最大值至少需要( )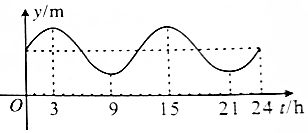

| A. | 6h | B. | 8h | C. | 12h | D. | 24h |
5.已知△ABC三个内角A、B、C所对的边分别为a、b、c,且3sinA=a,sinB=$\frac{3}{4}$,则b等于( )
| A. | $\frac{9}{4}$ | B. | 2 | C. | 3 | D. | 4 |
9.已知定认在R上的可导函数f(x)的导函数f′(x),若对于任意实数x,有f′(x)<f(x),且y=f(x)-1为奇函数,则不等式f(x)<ex的解集为( )
| A. | (0,+∞) | B. | (-∞,0) | C. | (-∞,e4) | D. | (e4,+∞) |
19.为了对2016年某校中考成绩进行分析,在60分以上的全体同学中随机抽取8位,他们的数学、物理、化学分数(折算成百分制)事实上对应如表:
(1)若规定80分以上为优秀,请填写如下2×2列联表,问是否有90%的把握认为是否优秀与科目有关;
(2)用变量y与x,z与x的相关系数说明物理与数学、化学与数学的相关程度;
(3)求y与x,z与x的线性回归方程(系数精确到0,01),当某位同学的数学成绩为50分时,估计其物理、化学两科的成绩.
参考公式:相关系数r=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sqrt{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}•\sum_{i=1}^{n}({y}_{i}-\overline{y})^{2}}$,
回归直线方程是:$\widehat{y}$=bx+a,其中b=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,a=$\overline{y}$-b$\overline{x}$,
参考数据:$\overline{x}$=77.5,$\overline{y}$=85,$\overline{z}$=81,$\sum_{i=1}^{8}$(xi-$\overline{x}$)2≈1050,$\sum_{i=1}^{8}$(yi-$\overline{y}$)2≈456,$\sum_{i=1}^{8}$(zi-$\overline{z}$)2≈550,≈688,$\sum_{i=1}^{8}$(xi-$\overline{x}$)(zi-$\overline{z}$)≈755,$\sqrt{1050}$≈32.4,$\sqrt{456}$≈21.4,$\sqrt{550}$≈23.5.
| 学生编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 数学分数x | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95 |
| 物理分数y | 72 | 77 | 80 | 84 | 88 | 90 | 93 | 95 |
| 化学分数z | 67 | 72 | 76 | 80 | 84 | 87 | 90 | 92 |
| 优秀 | 不优秀 | 合计 | |
| 数学 | |||
| 物理 | |||
| 合计 |
(3)求y与x,z与x的线性回归方程(系数精确到0,01),当某位同学的数学成绩为50分时,估计其物理、化学两科的成绩.
参考公式:相关系数r=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sqrt{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}•\sum_{i=1}^{n}({y}_{i}-\overline{y})^{2}}$,
回归直线方程是:$\widehat{y}$=bx+a,其中b=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,a=$\overline{y}$-b$\overline{x}$,
参考数据:$\overline{x}$=77.5,$\overline{y}$=85,$\overline{z}$=81,$\sum_{i=1}^{8}$(xi-$\overline{x}$)2≈1050,$\sum_{i=1}^{8}$(yi-$\overline{y}$)2≈456,$\sum_{i=1}^{8}$(zi-$\overline{z}$)2≈550,≈688,$\sum_{i=1}^{8}$(xi-$\overline{x}$)(zi-$\overline{z}$)≈755,$\sqrt{1050}$≈32.4,$\sqrt{456}$≈21.4,$\sqrt{550}$≈23.5.
4.某个命题与正整数有关,若当n=k(k∈N*)时该命题成立,那么可推得当n=k+1时该命题也成立,现已知当n=9时该命题不成立,那么可推得( )
| A. | 当n=10时,该命题不成立 | B. | 当n=10时,该命题成立 | ||
| C. | 当n=8时,该命题成立 | D. | 当n=8时,该命题不成立 |