题目内容
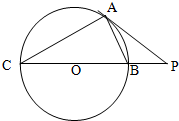 如图,CB是⊙O的直径,AP是⊙O的切线,AP与CB的延长线交于点P,A为切点.若PA=10,PB=5,则AB的长为
如图,CB是⊙O的直径,AP是⊙O的切线,AP与CB的延长线交于点P,A为切点.若PA=10,PB=5,则AB的长为考点:与圆有关的比例线段
专题:立体几何
分析:由已知得AP2=PB•PC,从而PC=20,BC=15,由已知得△PAB∽△PCA,从而
=
=
,由BC是⊙O的直径,得AC2+AB2=BC2=225,由此能求出AB的长.
| AB |
| AC |
| PA |
| PC |
| 1 |
| 2 |
解答:
解:∵CB是⊙O的直径,AP是⊙O的切线,
AP与CB的延长线交于点P,A为切点.PA=10,PB=5,
∴AP2=PB•PC,即100=5×PC,
解得PC=20,BC=15,
∵PA为⊙O的切线,
∴∠PAB=∠ACP,…(1分)
又∠P公用,∴△PAB∽△PCA,
∴
=
=
,
∵BC是⊙O的直径,
∴∠CAB=90°.
∴AC2+AB2=BC2=225,
∴AC=6
,AB=3
.
故答案为:3
.
AP与CB的延长线交于点P,A为切点.PA=10,PB=5,
∴AP2=PB•PC,即100=5×PC,
解得PC=20,BC=15,
∵PA为⊙O的切线,
∴∠PAB=∠ACP,…(1分)
又∠P公用,∴△PAB∽△PCA,
∴
| AB |
| AC |
| PA |
| PC |
| 1 |
| 2 |
∵BC是⊙O的直径,
∴∠CAB=90°.
∴AC2+AB2=BC2=225,
∴AC=6
| 5 |
| 5 |
故答案为:3
| 5 |
点评:本题考查线段长的求法,是中档题,解题时要认真审题,注意切割线定理和三角形相似的性质的合理运用.

练习册系列答案
相关题目
函数g(x)=2x2n-1+10x2-2x-1(n≥3,n∈N)在实数范围内的零点个数为( )
| A、0 | B、1 | C、2 | D、3 |
已知f(x)=
,且函数y=f(x)+x恰有3个不同的零点,则实数a的取值范围是( )
|
| A、(-∞,1] |
| B、(0,1] |
| C、(-∞,0] |
| D、(-∞,2] |