题目内容
已知函数f（x）=
，那么f（1）+f（2）+f（-2）+f（3）+f（-3）+f（4）+f（-4）= ．
|
考点：分段函数的应用
专题：计算题,函数的性质及应用
分析：利用f（x）=
，代入计算，即可得出结论．
|
解答：
解：∵f（x）=
，
∴f（1）=0，f（2）+f（-2）=
+
=1，
同理，f（3）+f（-3）=f（4）+f（-4）=1，
∴f（1）+f（2）+f（-2）+f（3）+f（-3）+f（4）+f（-4）=3
故答案为：3．
|
∴f（1）=0，f（2）+f（-2）=
| 4 |
| 1+4 |
| 2-2 |
| 1+2-2 |
同理，f（3）+f（-3）=f（4）+f（-4）=1，
∴f（1）+f（2）+f（-2）+f（3）+f（-3）+f（4）+f（-4）=3
故答案为：3．
点评：本题考查分段函数的应用，考查学生的计算能力，比较基础．
练习册系列答案
相关题目
已知函数f（x）=
，若f（1）=f（-1），则实数a的值等于（ ）
|
| A、2 | B、3 | C、4 | D、5 |
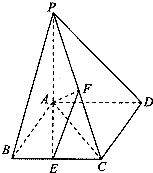如图，四棱锥P-ABCD的底面ABCD为菱形，PA⊥平面ABCD，∠ABC=60°，直线PC与底面ABCD所成的角为45°，E、F分别是BC、PC的中点．
如图，菱形ABCD与矩形BDEF所在平面互相垂直，∠BAD=
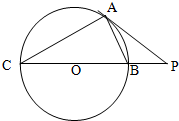如图，CB是⊙O的直径，AP是⊙O的切线，AP与CB的延长线交于点P，A为切点．若PA=10，PB=5，则AB的长为