题目内容
已知f(x)=
,且函数y=f(x)+x恰有3个不同的零点,则实数a的取值范围是( )
|
| A、(-∞,1] |
| B、(0,1] |
| C、(-∞,0] |
| D、(-∞,2] |
考点:函数零点的判定定理,分段函数的应用
专题:计算题,函数的性质及应用
分析:先根据当x≥0时,f(x)=f(x-1),可得当x≥0时,f(x)在[-1,0)重复的周期函数,再根据x∈[-1,0)时,y=a+x2+2x=-1+a+(x+1)2,对称轴x=-1,顶点(-1,-1+a),进而可进行分类:(1)如果a>1,函数y=f(x)-x至多有2个不同的零点;(2)如果a=1,则y有一个零点在区间(-1,0),有一个零点在(-∞,-1),一个零点是原点;(3)如果a<1,则有一个零点在(-∞,-1),y右边有两个零点,故可求实数a的取值范围.
解答:
解:因为当x≥0时,f(x)=f(x-1),所以所有大于等于0的x代入得到的f(x)
相当于在[-1,0)重复的周期函数,
x∈[-1,0)时,y=a+x2+2x=-1+a+(x+1)2,对称轴x=-1,顶点(-1,-1+a)
(1)如果a>1,函数y=f(x)+x至多有2个不同的零点;
(2)如果a=1,则y有一个零点在区间(-1,0),有一个零点在(-∞,-1),一个零点是原点;
(3)如果a<1,则有一个零点在(-∞,-1),y轴右边有两个零点,
故实数a的取值范围是(-∞,1].
故选A.
相当于在[-1,0)重复的周期函数,
x∈[-1,0)时,y=a+x2+2x=-1+a+(x+1)2,对称轴x=-1,顶点(-1,-1+a)
(1)如果a>1,函数y=f(x)+x至多有2个不同的零点;
(2)如果a=1,则y有一个零点在区间(-1,0),有一个零点在(-∞,-1),一个零点是原点;
(3)如果a<1,则有一个零点在(-∞,-1),y轴右边有两个零点,
故实数a的取值范围是(-∞,1].
故选A.
点评:本题重点考查函数的零点与方程根的关系,考查函数的周期性,有一定的难度.

练习册系列答案
相关题目
抛物线C1以双曲线C2:
-
=1(a>0,b>0)的右焦点F为焦点、左准线为准线,P为C1与C2的一个公共点,若直线PF恰好与x轴垂直,则双曲线C2的离心率所在区间为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、(1,
| ||
B、(
| ||
C、(2,
| ||
D、(
|
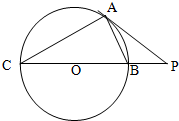 如图,CB是⊙O的直径,AP是⊙O的切线,AP与CB的延长线交于点P,A为切点.若PA=10,PB=5,则AB的长为
如图,CB是⊙O的直径,AP是⊙O的切线,AP与CB的延长线交于点P,A为切点.若PA=10,PB=5,则AB的长为