题目内容

已知函数f（x）=
log
1
2
x，x∈(0，
3
2
]
2x，x∈(
3
2
，+∞)
，解不等式f（x）＞3．
考点：分段函数的应用
专题：不等式的解法及应用
分析：根据分段函数的表达式，解不等式即可得到结论．
解答： 解：由分段函数的表达式函数f（x）=
log
1
2
x，x∈(0，
3
2
]
2x，x∈(
3
2
，+∞)
，不等式f（x）＞3可知，
若x∈(0，
3
2
]，则不等式f（x）＞3等价为log
1
2
x＞3，不等式的解为0＜x＜
1
8
，即解集为（0，
1
8
）．
若x∈(
3
2
，+∞)，则不等式f（x）＞3等价为2x＞3，解得x＞log23，不等式的解为：x∈(
3
2
，+∞)，
综上不等式的解集为（0，
1
8
）∪(
3
2
，+∞)．
点评：本题主要考查不等式的求解，根据分段函数的表达式分别进行求解和化简是解决本题的关键．
练习册系列答案
相关题目
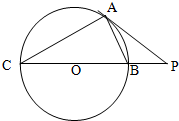如图，CB是⊙O的直径，AP是⊙O的切线，AP与CB的延长线交于点P，A为切点．若PA=10，PB=5，则AB的长为
 
．
设实数a，b，c满足a2+2b2+3c2=
3
2
，求
1
2a
+
1
4b
+
1
8c
的最小值．
a
=（1，1），
b
=（-1，0），则
ta
+
b
（t∈R）模的最小值是
 
．
已知实数x，y满足
x-y-1≤0
x≥1
2x+y-6≤0
，则当x+y=3时，目标函数z=
y
x
的取值范围是（　　）
A、[
4
7
，4]
B、[
1
2
，2]
C、[
1
2
，4]
D、[
4
7
，2]
在△ABC中，内角A，B，C对边分别是a，b，c，已知c=1，C=
π
3
．
（1）若cos（θ+C）=
5
13
，0＜θ＜π，求cosθ的值．
（2）若sinC+sin（A-B）=3sin2B，求△ABC的面积．
设
a
，
b
，则正确的是（　　）
A、
a
+
b
=
b
+
a
B、若
a
，
b
为两个单位向量，则
a
=
b
C、
a
-
b
=
b
-
a
D、若非零
a
，
b
共线，则
a
与
b
方向相同
在直角坐标系xOy中，以原点为极点，x轴的正半轴为极轴建立极坐标系，记ρ为极径，θ为极角，圆C：ρ=3cosθ的圆心C到直线l：ρcosθ=2的距离为
 
．
定义在{x|x∈R，x≠1}上的函数f（x）满足f（1-x）=-f（1+x），当x＞1时，f(x)=(
1
2
)x，则函数f（x）的图象与函数g（x）=
1
2
cosπ(x+
1
2
) (-3≤x≤5)的图象的所有交点的横坐标之和等于（　　）
A、4B、6C、8D、10

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网