题目内容
从编号为1,2,3,4,5的五个大小完全相同的小球中随机取出3个,用ξ表示其中编号为奇数的小球的个数,则Eξ= .
考点:离散型随机变量的期望与方差
专题:概率与统计
分析:由已知得ξ=1,2,3,分别求出相应的概率,由此能求出Eξ.
解答:
解:由已知得ξ=1,2,3,
P(ξ=1)=
=
,
P(ξ=2)=
=
,
P(ξ=3)=
=
∴Eξ=1×
+2×
+3×
=
.
故答案为:
.
P(ξ=1)=
| ||||
|
| 3 |
| 10 |
P(ξ=2)=
| ||||
|
| 6 |
| 10 |
P(ξ=3)=
| ||
|
| 1 |
| 10 |
∴Eξ=1×
| 3 |
| 10 |
| 6 |
| 10 |
| 1 |
| 10 |
| 9 |
| 5 |
故答案为:
| 9 |
| 5 |
点评:本题考查离散型随机变量的数学期望的求法,是中档题,解题时要认真审题.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案
相关题目
设双曲线
-
=1(a>0,b>0)的左、右焦点分别是F1、F2,过点F2的直线交双曲线右支于不同的两点M、N.若△MNF1为正三角形,则该双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
对于非零向量
,
,定义一种向量积:
•
=
.已知非零向量
,
的夹角θ,∈(0,
),且
•
,
•
都在集合{
|n∈Z}中.则
•
=( )
| α |
| β |
| α |
| β |
| ||||
|
| a |
| b |
| π |
| 4 |
| a |
| b |
| b |
| a |
| n |
| 2 |
| a |
| b |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
抛物线C1以双曲线C2:
-
=1(a>0,b>0)的右焦点F为焦点、左准线为准线,P为C1与C2的一个公共点,若直线PF恰好与x轴垂直,则双曲线C2的离心率所在区间为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、(1,
| ||
B、(
| ||
C、(2,
| ||
D、(
|

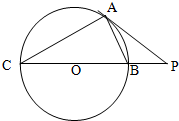 如图,CB是⊙O的直径,AP是⊙O的切线,AP与CB的延长线交于点P,A为切点.若PA=10,PB=5,则AB的长为
如图,CB是⊙O的直径,AP是⊙O的切线,AP与CB的延长线交于点P,A为切点.若PA=10,PB=5,则AB的长为