题目内容
将正奇数排列如图所示的形式,其中第i行第j个数表示aij(i∈N*,j∈N*),例如a32=9,若aij=2013,则i+j= .
1
3 5
7 9 11
13 15 17 19.
1
3 5
7 9 11
13 15 17 19.
考点:归纳推理
专题:推理和证明
分析:分析正奇数排列的正三角图表知,第i行(其中i∈N*)有i个奇数,且从左到右按从小到大的顺序排列,则2013是第1007个奇数,由等差数列的知识可得,它排在第几行第几个数.
解答:
解:根据正奇数排列的正三角图表知,2013是第1007个奇数,应排在i行(其中i∈N*),
则1+2+3+…+(i-1)=
<1007①,且1+2+3+…+i=
>1007②;
验证i=45时,①②式成立,所以i=45;
第45行第1个奇数是2×
+1=1981,而1981+2(j-1)=2013,∴j=17;
所以,2013在第45行第17个数,则i+j=62;
则1+2+3+…+(i-1)=
| i(i-1) |
| 2 |
| i(i+1) |
| 2 |
验证i=45时,①②式成立,所以i=45;
第45行第1个奇数是2×
| 44×45 |
| 2 |
所以,2013在第45行第17个数,则i+j=62;
点评:本题考查了等差数列的应用问题,解题时可以根据题目中的数量关系,合理地建立数学模型,运用所学的知识,解答出结果.

练习册系列答案
相关题目
已知F1、F2分别是双曲线
-
=1(a>0,b>0)的左右焦点,其右支上一点P,满足|PF1|=3,实轴长为1,M是y轴上一点,则
•(
-
)=( )
| x2 |
| a2 |
| y2 |
| b2 |
| PM |
| PF1 |
| PF2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知实数x,y满足
,则当x+y=3时,目标函数z=
的取值范围是( )
|
| y |
| x |
A、[
| ||
B、[
| ||
C、[
| ||
D、[
|
 如图,菱形ABCD与矩形BDEF所在平面互相垂直,∠BAD=
如图,菱形ABCD与矩形BDEF所在平面互相垂直,∠BAD=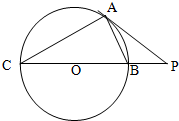 如图,CB是⊙O的直径,AP是⊙O的切线,AP与CB的延长线交于点P,A为切点.若PA=10,PB=5,则AB的长为
如图,CB是⊙O的直径,AP是⊙O的切线,AP与CB的延长线交于点P,A为切点.若PA=10,PB=5,则AB的长为