题目内容
函数g(x)=2x2n-1+10x2-2x-1(n≥3,n∈N)在实数范围内的零点个数为( )
| A、0 | B、1 | C、2 | D、3 |
考点:根的存在性及根的个数判断
专题:函数的性质及应用
分析:对函数f(x)=2x2n-1+10x2-2x-1进行求导,求得函数的极值,单调性,判断零点个数,注意计算时整体代换.
解答:
解:∵函数f(x)=2x2n-1+10x2-2x-1,
∴f′(x)=2(2n-1)x2n-2+20x-2=2[(2n-1)x2n-2+10x-1]
在f′(x)=0时,
f(x)=2x2n-1+10x2-2x-1=
x[(2n-1)x2n-2+10x-1]+
x2-
x-1=
x2-
x-1,
由于判别式△>0,所以,f(x)的极小值是负数.
又因为当x趋向于负无穷和正无穷时均为无穷大,
所以,零点有3个;
故选D.
∴f′(x)=2(2n-1)x2n-2+20x-2=2[(2n-1)x2n-2+10x-1]
在f′(x)=0时,
f(x)=2x2n-1+10x2-2x-1=
| 2 |
| 2n-1 |
| 10(2n-3) |
| 2n-1 |
| 2(2n-3) |
| 2n-1 |
| 10(2n-3) |
| 2n-1 |
| 2(2n-3) |
| 2n-1 |
由于判别式△>0,所以,f(x)的极小值是负数.
又因为当x趋向于负无穷和正无穷时均为无穷大,
所以,零点有3个;
故选D.
点评:本题考查函数零点判定定理和利用导数研究函数的单调性和极值等问题,同时考查学生灵活应用知识分析解决问题的能力和计算能力.

练习册系列答案
相关题目
抛物线C1以双曲线C2:
-
=1(a>0,b>0)的右焦点F为焦点、左准线为准线,P为C1与C2的一个公共点,若直线PF恰好与x轴垂直,则双曲线C2的离心率所在区间为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、(1,
| ||
B、(
| ||
C、(2,
| ||
D、(
|
设
,
,则正确的是( )
| a |
| b |
A、
| ||||||||
B、若
| ||||||||
C、
| ||||||||
D、若非零
|
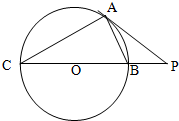 如图,CB是⊙O的直径,AP是⊙O的切线,AP与CB的延长线交于点P,A为切点.若PA=10,PB=5,则AB的长为
如图,CB是⊙O的直径,AP是⊙O的切线,AP与CB的延长线交于点P,A为切点.若PA=10,PB=5,则AB的长为