题目内容
设函数f(x)=|x-1|+|x-a|的图象关于直线x=2对称.
(1)求a的值;
(2)作出y=f(x)的图象.
(1)求a的值;
(2)作出y=f(x)的图象.
考点:函数的图象
专题:函数的性质及应用
分析:直接利用两个绝对值相加的函数的图象的对称轴所特有的结论,即可求a的值.
解答:
 解:(1)由于函数f(x)=|x-1|+|x-a|的图象关于直线x=
解:(1)由于函数f(x)=|x-1|+|x-a|的图象关于直线x=
对称,
而已知函数f(x)=|x-1|+|x-a|的图象关于直线x=2对称,
故有
=2,解得a=3.
(2)由(1)可得f(x)=|x-1|+|x-3|=
,它的图象如图所示:
 解:(1)由于函数f(x)=|x-1|+|x-a|的图象关于直线x=
解:(1)由于函数f(x)=|x-1|+|x-a|的图象关于直线x=| a+1 |
| 2 |
而已知函数f(x)=|x-1|+|x-a|的图象关于直线x=2对称,
故有
| a+1 |
| 2 |
(2)由(1)可得f(x)=|x-1|+|x-3|=
|
点评:本题主要考查两个绝对值相加的函数的图象特点,在平时做题过程中,要善于运用总结的结论和性质,做小题时节约时间,属于基础题.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
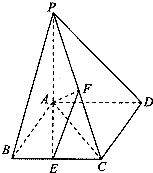 如图,四棱锥P-ABCD的底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,直线PC与底面ABCD所成的角为45°,E、F分别是BC、PC的中点.
如图,四棱锥P-ABCD的底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,直线PC与底面ABCD所成的角为45°,E、F分别是BC、PC的中点.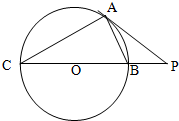 如图,CB是⊙O的直径,AP是⊙O的切线,AP与CB的延长线交于点P,A为切点.若PA=10,PB=5,则AB的长为
如图,CB是⊙O的直径,AP是⊙O的切线,AP与CB的延长线交于点P,A为切点.若PA=10,PB=5,则AB的长为