题目内容

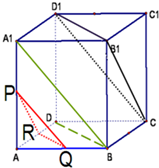如图所示，已知正方体ABCD-A1B1C1D1中，P、Q、R分别为A1A、AB、AD的中点，求证：平面PQR∥平面CB1D1．
考点：平面与平面平行的判定
专题：证明题,空间位置关系与距离
分析：根据三角形中位线定理，结合正方体的几何特征，我们易得QR∥B1D1，同理可得PQ∥D1C，进而根据面面平行的判定定理即可得到平面PQR∥平面CB1D1．
解答： 证明：在正方体ABCD-A1B1C1D1中，对角线BD∥B1D1，
∵Q、R分别为AB、AD的中点，
∴QR∥BD
∴QR∥B1D1，
同理可证：PQ∥D1C，
又∵QR∩PQ=Q，B1D1∩D1C=D1，
∴平面PQR∥平面CB1D1．
点评：本题考查的知识点是平面与平面平行的判定，熟练掌握正方体的几何特征，分析出其中线段的平行关系，结合面面平行的判定定理，对结论进行论证是解答本题的关键．
练习册系列答案
相关题目
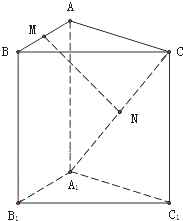在三棱柱ABC-A1B1C1中，M、N分别是AB、A1C的中点，求证：MN∥平面BCB1C1．
已知椭圆E1：
x2
a2
+
y2
b2
=1（a＞b＞0）椭圆E2的中心在坐标原点，焦点在x轴上，其长轴长和短轴长分别是椭圆E1长轴长和短轴长的
λ
倍（λ＞0，λ≠1）．
（Ⅰ）求椭圆E2的方程；并证明椭圆E1，E2的离心率相同；
（Ⅱ）当λ=2时，设M，N是椭圆E1上的两个点，OM，ON的斜率分别是kOM，kON，且kOM•kON=-
b2
a2
（O是坐标原点），若OMPN是平行四边形，证明：点P在椭圆E2上．
数列{an}各项均为正数，首项为a，对任意正整数n，an•an+1=
4n
2
恒成立．
（Ⅰ）若数列{an}为等比数列，求实数a的值；
（Ⅱ）记bn为数列{an}的前2n项的和，若对任意正整数n，不等式bn≤
11
4
（4n-1）恒成立，求实数a的取值范围．
在平面直角坐标系xOy中，将从点M出发沿纵、横方向到达点N的任一路径称为M到N的一条“折线路径”，所有“折线路径”中长度最小的称为M到N的“折线距离”．如图所示的路径MD1D2D3N与路径MEN都是M到N的“折线路径”．某地有三个居民区分别位于平面xOy内三点A（-8，1），B（5，2），C（1，14），现计划在这个平面上某一点P（x，y）处修建一个超市．
（1）请写出点P到居民区A的“折线距离”d的表达式（用x，y表示，不要求证明）；
（2）为了方便居民，请确定点P的位置，使其到三个居民区的“折线距离”之和最小．
平面内一动点P到点F（2，0）的距离比它到直线x+3=0的距离少1
（1）求动点P的轨迹方程；
（2）过点F（2，0）作一条倾斜角为α的直线，交抛物线于A（x1，y1），B（x2，y2）两点，线段AB的中点是M，直线OM的斜率kOM=f（α），求kOM=f（α）的取值范围．
已知各项均为正数的数列{an}满足an+12=2an2+anan+1，且a2+a4=2a3+4，其中n∈N*．
（1）求数列{an}的通项公式；
（2）设数列{bn}满足bn=
nan
(2n+1)•2n
，是否存在正整数m，n（1＜m＜n），使得b1，bm，bn成等比数列？若存在，求出所有的m、n的值；若不存在，请说明理由．
（3）令cn=
(n+1)2+1
n(n+1)an+2
，记数列{cn}的前n项和为Sn（n∈N*），证明：
5
16
≤Sn＜
1
2
．
过一定点P，与已知直线a所成的角为60°的直线有
 
条．
若有穷数列a1，a2，…an（n∈N*）满足a1=an，a2=an-1，…，an=a1，即ai=an-i+1（其中i∈N*，i≤n），就称该数列为“对称数列”．若{bn}是项数为2k-1（k∈N*）的“对称数列”，且bk，bk+1，b2k-1构成首项为50，公差为-4的等差数列，其前2k-1项和为S2k-1，则S2k-1的最大值为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网